ただひたすらに（１次元）フーリエ変換．

意外と何やってるかわからなくなるので備忘録も兼ねて．

フーリエ変換（Fourier transform; FT）は、時間(or空間)軸と周波数軸の変換．

基本のコードは以下．

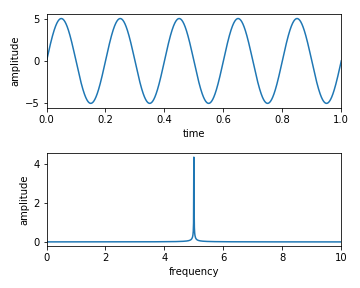
Code-01

import numpy as np
from scipy.fftpack import fft
import matplotlib.pyplot as plt

# parameters
N = 2**20 # data number
dt = 0.0001 # data step [s]
f1, f2 = 5, 8 # frequency[Hz]
A1, A2 = 5, 0 # Amplitude
p1, p2 = 0, 0 # phase

t = np.arange(0, N*dt, dt) # time
freq = np.linspace(0, 1.0/dt, N) # frequency step

y = A1*np.sin(2*np.pi*f1*t + p1) + A2*np.sin(2*np.pi*f2*t + p2) 

yf = fft(y)/(N/2) # 離散フーリエ変換&規格化

plt.figure(2)
plt.subplot(211)
plt.plot(t, y)
plt.xlim(0, 1)
plt.xlabel("time")
plt.ylabel("amplitude")

plt.subplot(212)
plt.plot(freq, np.abs(yf))
plt.xlim(0, 10)
#plt.ylim(0, 5)
plt.xlabel("frequency")
plt.ylabel("amplitude")
plt.tight_layout()
plt.savefig("01")
plt.show()

周期5Hz sin波

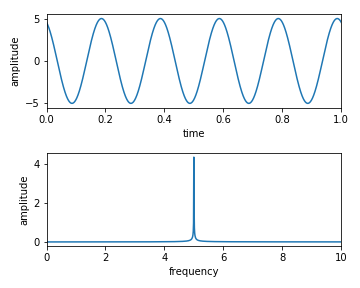
Code-02

# parameters
N = 2**20 # data number
dt = 0.0001 # data step [s]
f1, f2 = 5, 8 # frequency[Hz]
A1, A2 = 5, 0 # Amplitude
p1, p2 = 2, 0 # phase

y = A1*np.sin(2*np.pi*f1*t + p1) + A2*np.sin(2*np.pi*f2*t + p2)

周期5　位相シフト2
もちろん周波数も振幅も変わらない

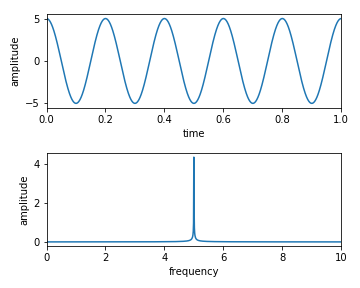
Code-03

# parameters
f1, f2 = 5, 8 # frequency[Hz]
A1, A2 = 5, 0 # Amplitude
p1, p2 = 0, 0 # phase

y = A1*np.cos(2*np.pi*f1*t + p1) + A2*np.sin(2*np.pi*f2*t + p2)

周期5　cos波
周波数も振幅も変わらない

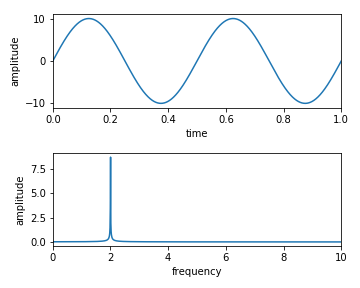
Code-04

# parameters
f1, f2 = 2, 8 # frequency[Hz]
A1, A2 = 10, 0 # Amplitude
p1, p2 = 0, 0 # phase

y = A1*np.sin(2*np.pi*f1*t + p1) + A2*np.sin(2*np.pi*f2*t + p2)

周波数2 振幅10

周波数については，ほぼ正確にわかる
一方で振幅は誤差がありそう．

Code-05

# parameters
f1, f2 = 5, 8 # frequency[Hz]
A1, A2 = 5, 3 # Amplitude
p1, p2 = 0, 0 # phase

y = A1*np.sin(2*np.pi*f1*t + p1) + A2*np.sin(2*np.pi*f2*t + p2)

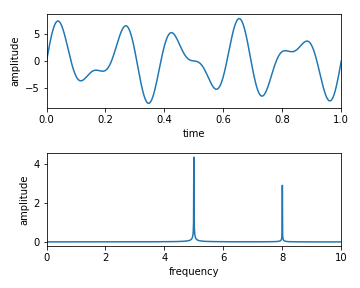
周波数5 振幅5 & 周波数8 振幅3
波の形状は複雑だが周波数は求められている．

Code-06

# parameters
f1, f2 = 5, 0 # frequency[Hz]
A1, A2 = 5, 0 # Amplitude

y = A1*np.sin(2*np.pi*f1*t)**2

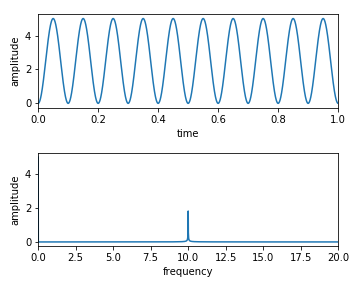
周波数5 $\sin^{2}$ 波
周波数5でも，2乗したら実質の周波数は2倍の10

Code-07

# parameters
y = np.zeros(N)*dt
y[50000] =5
y[N-50000]=5

yf = ifft(y)*(N/2) # 逆フーリエ変換&規格化

逆フーリエ変換
周波数・振幅はあってる．cos波になった．

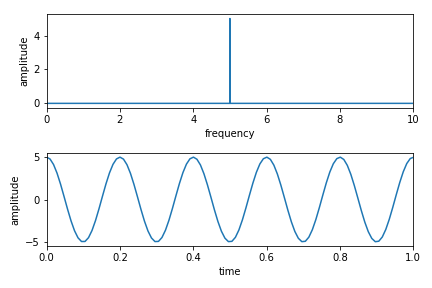
周波数軸から時間軸に直すときは，(対称性を考慮して)2点打つ．

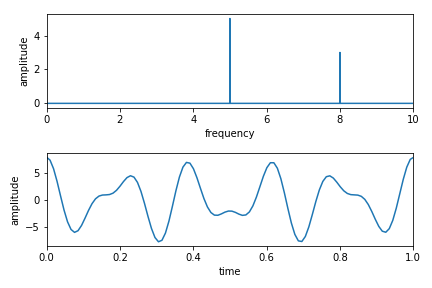
Code-08

# parameters
y = np.zeros(N)*dt
y[int(f1/dt)] =5
y[N-int(f1/dt)] =5
y[int(f2/dt)] =3
y[N-int(f2/dt)] =3
yf = ifft(y)*(N/2) # 逆フーリエ変換&規格化

2点打つ．

Code-09

from scipy.special import jv

y = jv(0, t)

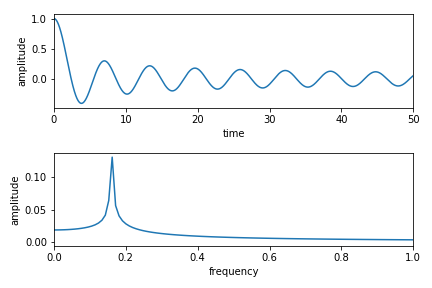
第一種ベッセル関数を試してみる．
完全に周期的な関数ではないので，ピークは確認されたが，すそを引いた周波数の結果が得られた．

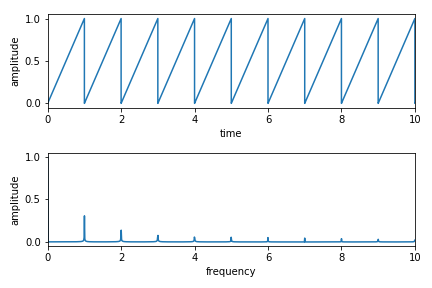
Code-10

y = t - np.floor(t)

$y = x - | x |$
これも一種の周期関数
「整数値」ごとに周期的なピーク

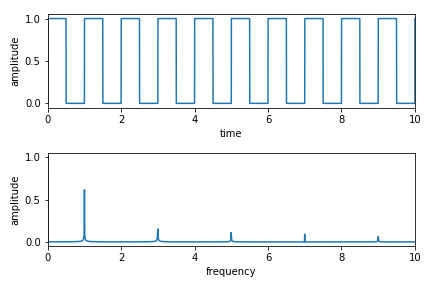
Code-11

y = np.ceil(t) - np.round(t)

$y = | x + 1 | - r o u n d (x)$
奇数ごとに周期的なピーク

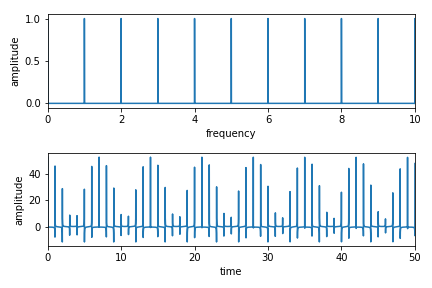
Code-12

y = np.zeros(N)*dt
y[::10000] =1

周期1ごとに値1
ちょっと変わった感じの関数が得られた．

周波数解析に使われるフーリエ変換をひたすらにやりました。

いつか誰かの役に立てばと思います。

以上です。

参考文献

Discrete Fourier transforms (scipy.fftpack)
https://docs.scipy.org/doc/scipy/reference/fftpack.html

【Python】ただひたすらにフーリエ変換【備忘録】

参考文献