はじめに
この記事は機械学習において、深層学習に匹敵する表現力を持つ、
ガウス過程について概説するものです。
構成は
- ガウス過程とは?
- ガウス過程の仕組み
- ガウス過程の実践
です。
ガウス過程とは?
性能
深層学習と同じ性能を持つことが証明されています。
(深層学習がどんなネットワーク構造を持っていても。
CNN、Attention、BERT、それらの組み合わせ、でも)
証明記事へのリンク https://twitter.com/Spike23645/status/1202943370068234245?s=20
歴史と計算量
数学、確率過程の分野で、ガウス過程の関数近似力が、中間層無限の3層パーセプトロンに匹敵することは、古くから知られていました。
それが、アルゴリズムの改善(主にWilson氏の「愛の三部作」:KISS-GP、SKI、LOVE←本当にこういう名前です)によって、
計算量が爆発的に減り(たとえば学習にO(n+m)以下、n入力データ数、m推測点数)、今に至ります。
確率過程から機械学習へ
ランダムウォークなどで用いられる確率過程。
ガウス過程はもともとこの一種です(インデックス、時間相当の横軸tの時間発展と、縦軸の値yの関係が、数式であらわされるもの)
確率過程は、インデックス(横軸)を入力データxにしても良いので、そうすると、
入力データが前後した時の、出力データyの関係を表せます。
つまり、そこに、観測値と推定値との差を低くするよう、
パラメータを調節するオプティマイザをつけてやれば。
確率過程であるガウス過程は、学習器になるわけです。
ガウス過程の仕組み
信頼度の表示
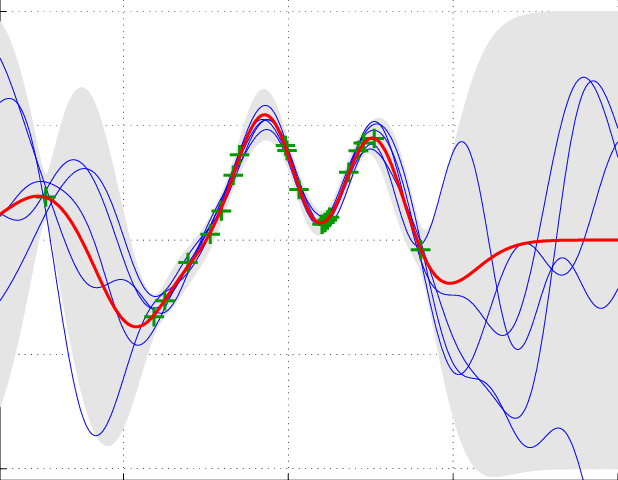
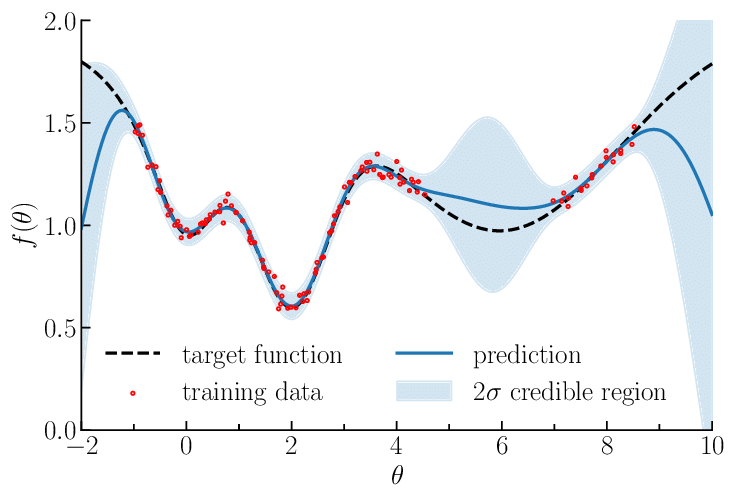
図のように、赤い点で観測データが入力されたとき、青い線が出力となる推測した値です。
黒い線は実際の真の値。
水色の帯の部分が信頼区間を表しています(これがきちんと計算されるのは、「精度」「SOTA」という言葉がひとり歩きしがちの深層学習とは異なる特徴です)
具体的には、上の図の、
- 赤い観測点がそもそも少ない区間
- 同じxの値でも、y軸の値のぶれが大きい区間
これらにおいて、信頼度を示す水色の帯が広がっているのがわかると思います。
このために、
- 観測データが足りないところ
- 観測データが信頼できない/ノイズが大きいところ
が視覚的にわかり、
- 観測データを、特にどこにおいて増やすべきか
- 観測データのノイズが大きいので、センサや計測法を変えるべきか
が明示的にわかります。
実際にデータ活用をするうえで(研究やビジネスにも有効な)定量的な指針を与えてくれるというわけです!
ガウス過程の実践
インストール
Python、PyTorchのインストールは前提とします(他に山ほど参考記事があるでしょうし)
ここでは、GPyTorch(ガウス過程ライブラリ)のインストールを説明します
(Pyroから動かす方法もありますが、今回はそうします)
Python>=3.6、PyTorch>=1.3の依存関係を満たしている場合、
pip install gpytorch
か
conda install gpytorch -c gpytorch
でインストールできます。
あとは、公式ドキュメント
https://gpytorch.readthedocs.io/en/latest/examples/01_Exact_GPs/Simple_GP_Regression.html
の、サイン関数にノイズを加えたものの回帰を行う、をご覧ください。
それからのさらに応用的な記事は......
これから書きます......(お待ちください)
終わりに
ガウス過程、いかがだったでしょうか。
実は、私のTwitterアカウントから検索すれば、ここに書いたことはほとんど書いてあります(この記事はまとめです)
また、前の記事
の終わりに「リプはTwitterのほうが反応速いです」
私のTwitterアカウント https://twitter.com/Spike23645
とか書いてしまいましたが、こちらQiitaも(できるだけ)見るようにするので、
忌憚のないご意見お願いいたします。
間違いあれば訂正いたします。対応遅れたら申し訳ありません。
なお、これから私は、
ガウス過程、パーシステントホモロジー・Topological Data Analysis、深層学習機構の代数による記述、数理ファイナンスと力学系、などの記事を連載予定です!
あと、はてぶにもミラー作るかもしれません(?)
運用体制はおいおい考えます......