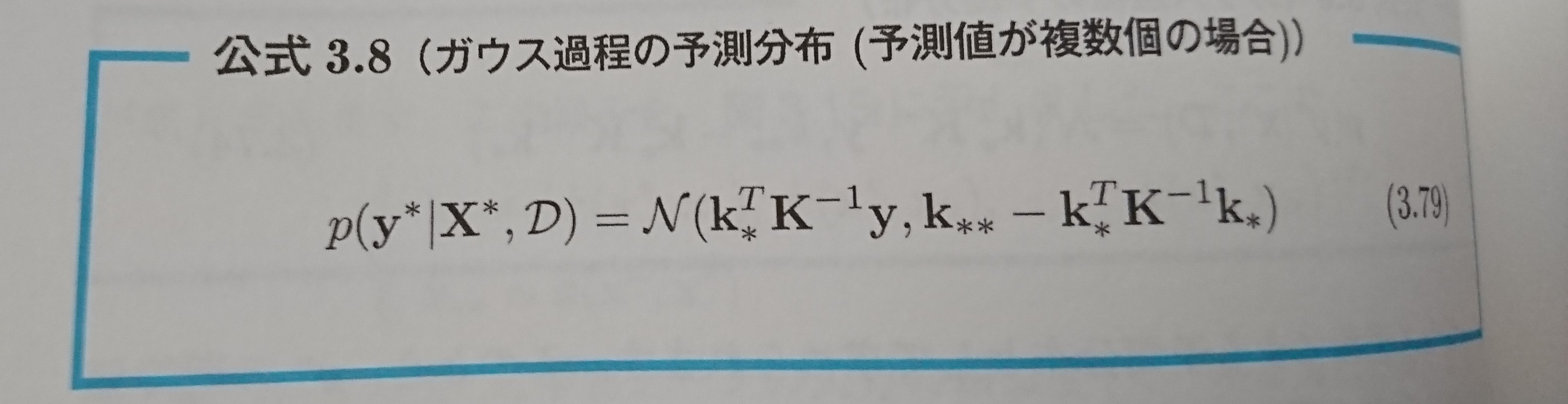はじめに
構成
この記事は
- 前半:観測データと推測点
- 後半:ベイズ更新と共分散行列
と分かれています。
(ゆるい)前提
一応、前記事
を読んでいること前提でお話しします。
ただ、記事の独立性はある程度あるので、
わからない単語があればそちらを見るようにする程度で(多分)結構です。
前半:観測データと推測点
要するに
ガウス過程はいかに、
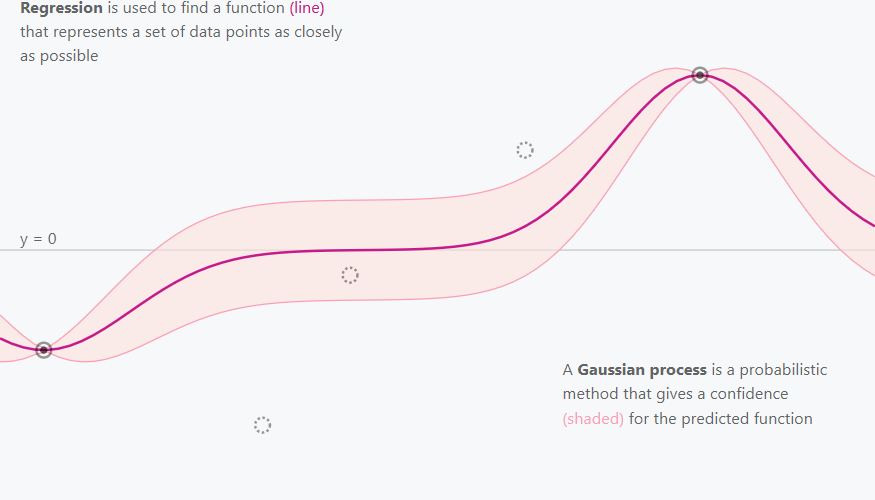
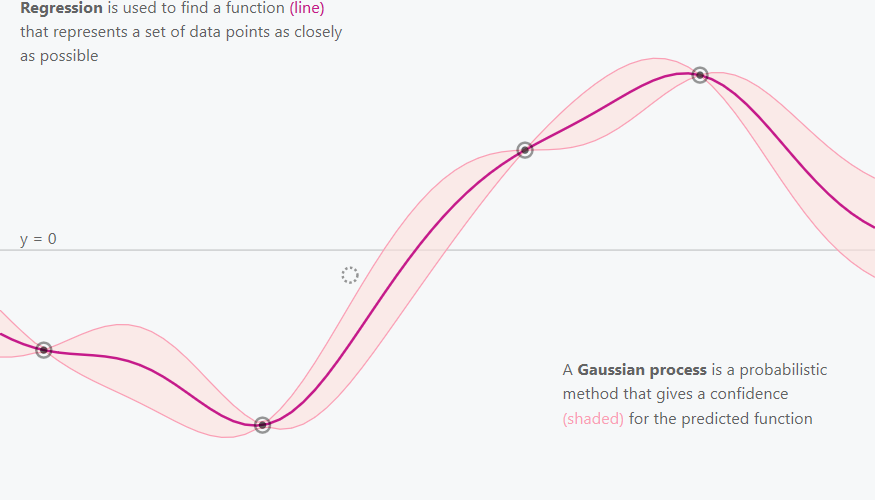
図1→図2へと、どのように推測の信頼度を向上させていくか?
(図でいうピンク色の、推定の信頼区間の幅を減らしていくか?)
というお話です。
図1 図2 https://distill.pub/2019/visual-exploration-gaussian-processes/
前半では、入力データセットを一回だけ入れて、
ガウス過程がどう変化するかを観ます。
(学習の過程は後半に書きます)
データ入力する前
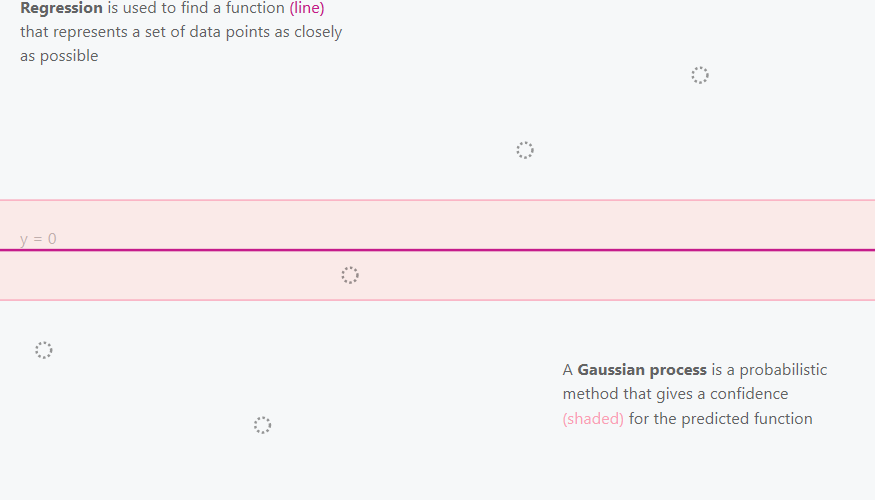
データ入力前の、ガウス過程の出力はこうなります
図3 https://distill.pub/2019/visual-exploration-gaussian-processes/
まあ……当然ですね。直線。
事前分布が多変量ガウス分布、平均0で正規化されているので。
この直線が、実際はどう生まれたのか?
どう計算されたか?
について理解するため、
ガウス過程の理論的な側面に少し触れます。
ベイズ的背景
そもそも、ガウス過程はベイズ系機械学習です。
ここで、ベイズ系機械学習という言葉で意味しているのは。
- 事前分布
- 尤度計算
- ベイズ更新(学習) 「事後分布 = 尤度×事前分布」
となっているもののことです。
これに、ガウス過程も属します。
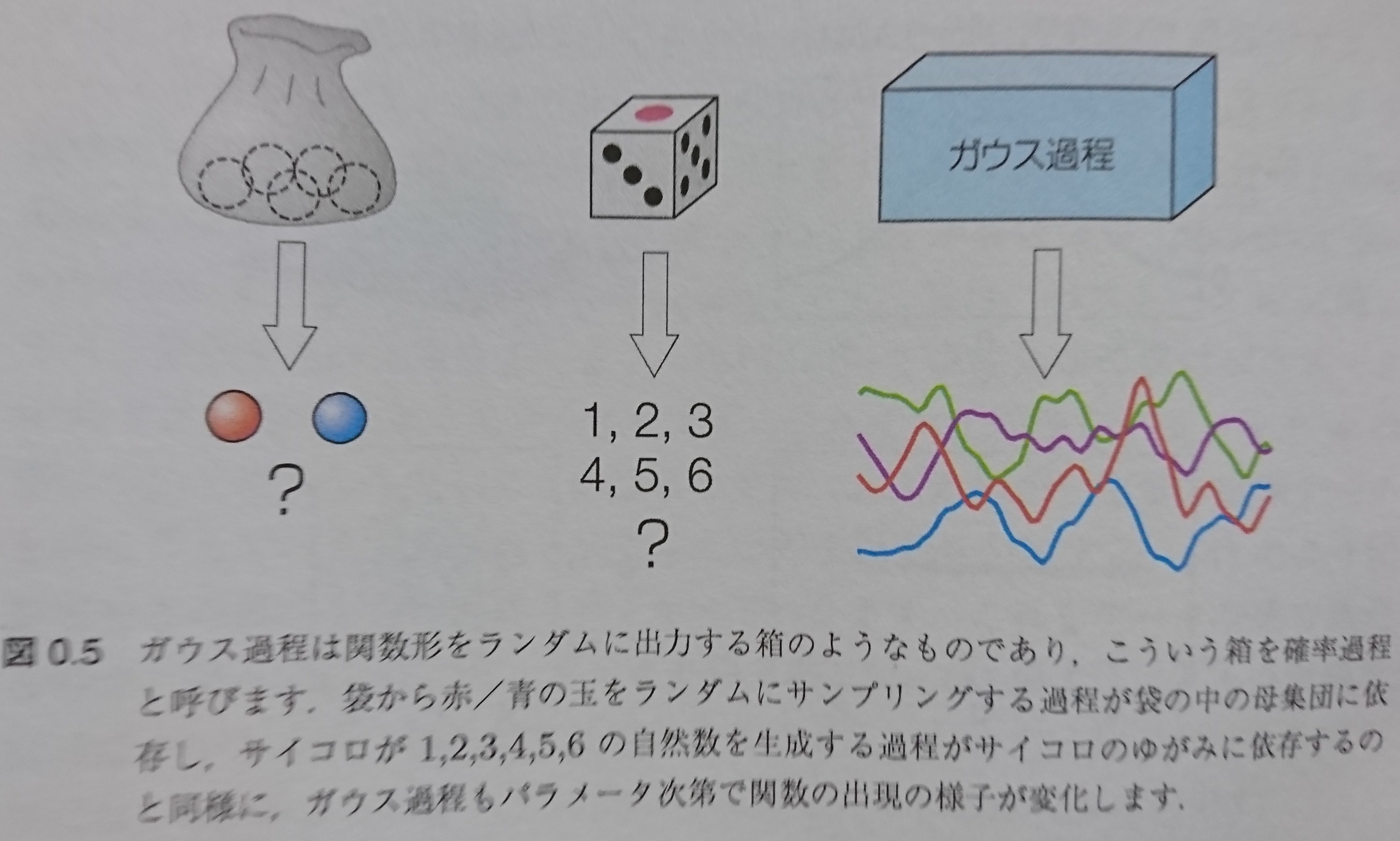
ベイズ系機械学習と、ガウス過程について、絵で見て見ると
下のようになります。
(ベイズの、主観的確率、の説明に
よく赤い球と青い球が入った袋、サイコロが使われます)
図4 持橋『ガウス過程と機械学習』より
つまり、事前分布に従い取り出すものが、
- 赤い球や青い球
- サイコロの目
- 関数の束
になっているのが、
ガウス過程と言えます。
ここでいう関数の束、の「関数」とは、
「多変量ガウス分布」、の一次元の場合。
なのですが、
「多変量ガウス分布」について、
詳しくは、いずれ触れます。
未来の記事への参照(予定)
今回は「観て理解」のコンセプトなので、
参考の図を貼っておきます。
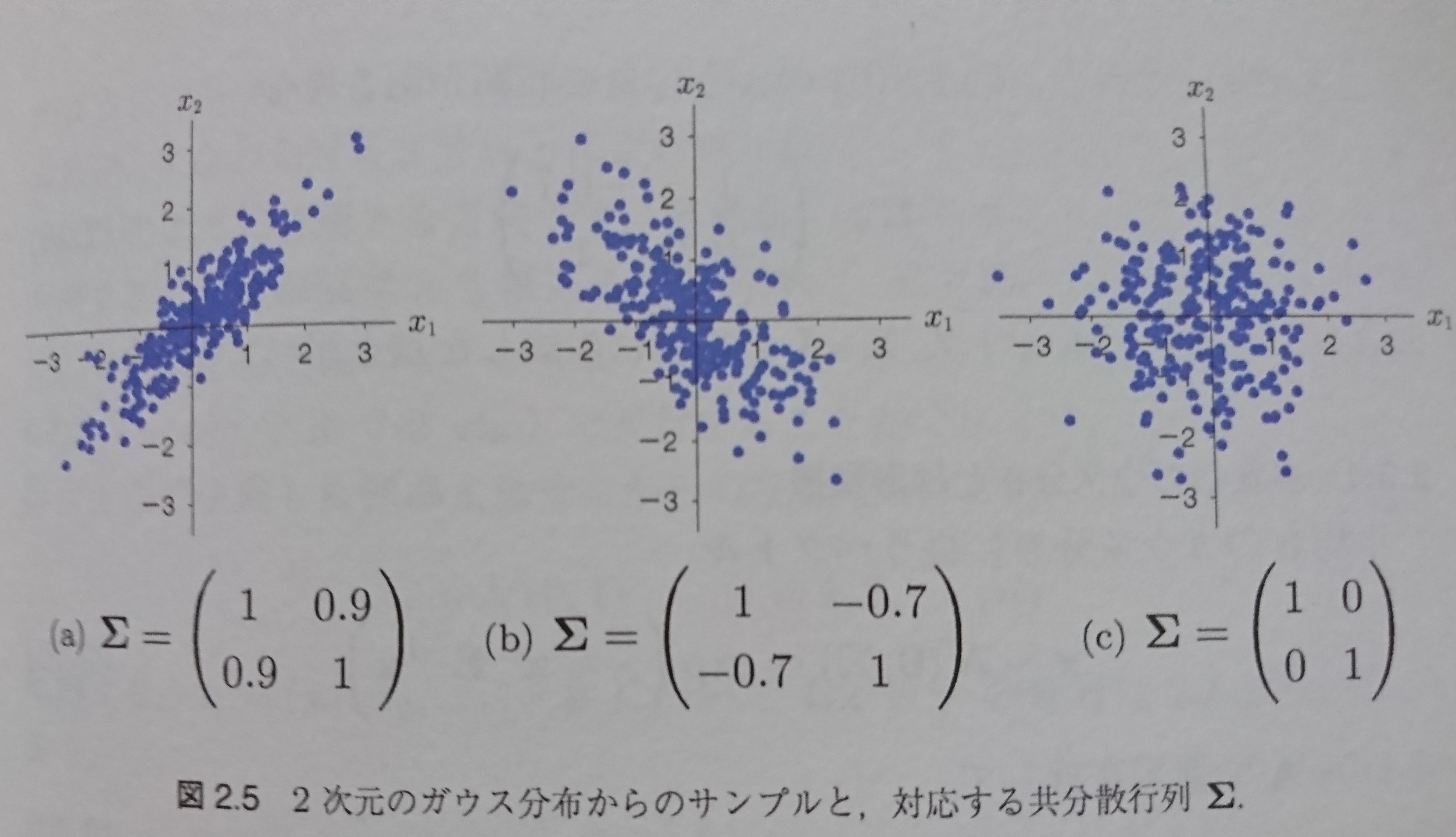
下図5は、二次元の場合の、多変量ガウス分布の例です。
(正確にはそれからのサンプリングですが)
図5 持橋『ガウス過程と機械学習』より
共分散行列(ガウス過程の文脈では、カーネルとも言います)
のΣの値によって、散布図が変わっているのがわかると思います。
後半:ベイズ更新と共分散行列
さきほど、
共分散行列=カーネル
と言いました。
- その共分散行列とは何か、
- ベイズ更新に従う変化について、理解しましょう!
共分散行列(=カーネル)
ガウス過程が「関数の箱」から取り出す、
多変量ガウス分布とは。
n個のガウス分布(正規分布)が、
その学習時点での共分散行列(=カーネル)
に従って相関して出てきたもの
を指します。
つまり、ガウス過程は
ベイズ更新するカーネル法
とも言えます。
ここが、共分散行列が、ガウス過程で「カーネル」と
呼ばれるゆえんでもあります。
学習の前は、大抵RBFカーネル
(Radial Basis Function = ガウス分布 なので、ガウスカーネルともいう)
を、共分散行列の初めの値として設定することが多いです。
(ガウス過程の共分散行列がさらにガウス分布カーネル、というと「ガウス」という
言葉が出過ぎて混乱を招くので、RBFカーネルということが多いです)
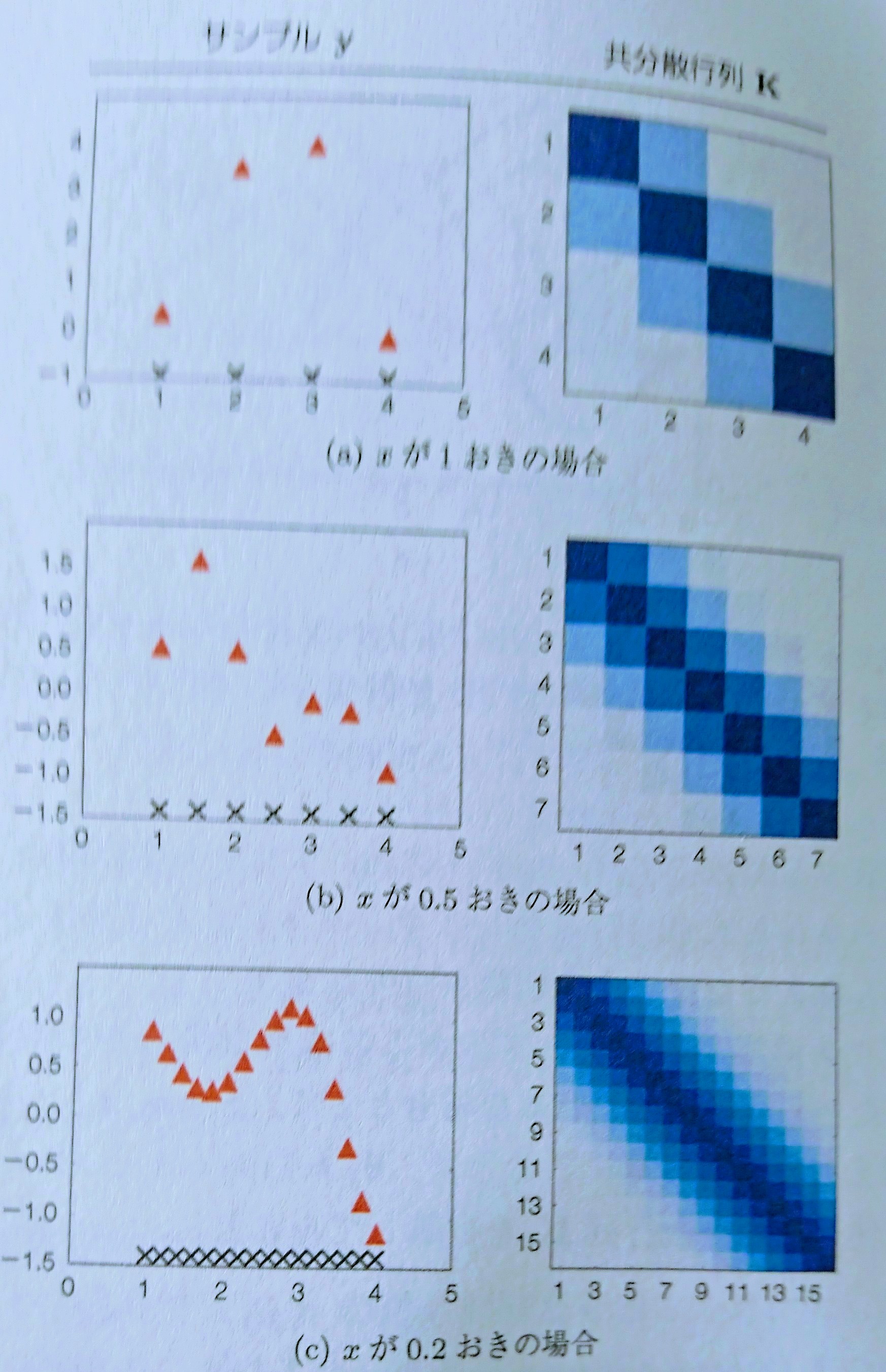
学習をまだしていないRBFカーネルと、その出力のガウス過程は、
図6のようになります。
図6 持橋『ガウス過程と機械学習』
n次共分散行列、のnの値が大きいほど、
RBFカーネルは、
滑らかな関数を出す(そこからのサンプルが取れる)ことが
観て分かると思います。
(実際、RBFカーネルを共分散行列とする多変量ガウス分布は、
級です)
学習法(視覚的理解)
共分散行列の値をベイズ更新していくのが、
ガウス過程における「学習」です。
いわゆるベイズ更新とは、
事後分布=尤度*事前分布
で表されるものです。
これにより、事前分布、事後分布のガウス過程が変わっていきます。
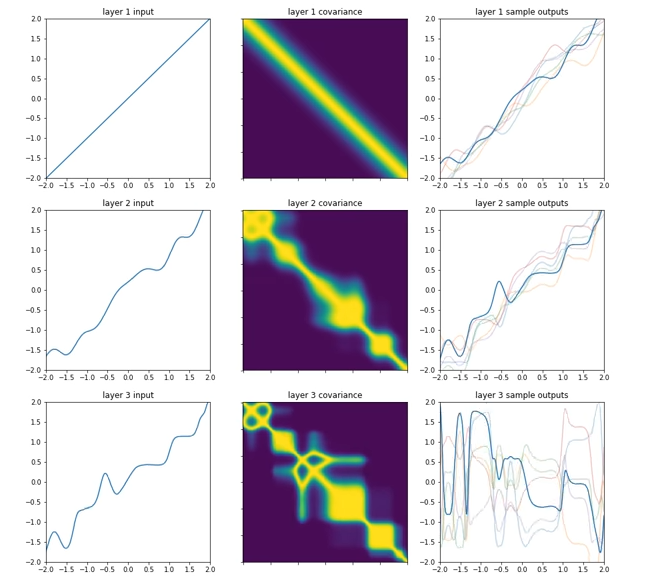
ガウス過程のもともとRBFカーネルだった共分散行列が
変化していくと、例えば次のようになります。
図7 (実は、そのうち紹介する「深層ベイズ学習」の一種の、学習過程動画のスクショです)https://youtu.be/Tjjq2fCY8Fc
学習法のベイズ更新については、
次回以降にまわします(今回は視覚的理解をする記事なので)
さらっとだけ具体的な数式と、
学習過程のガウス過程の出力に触れると、
図8、図9 持橋『ガウス過程と機械学習』
おわりに
記事が長くなりすぎると良くないので、
数式的な理解は次回以降に飛ばします。
あと、深層ベイズについても
(最後の出力がガウス過程だったり、ガウス過程を複数段重ねたりします)
いずれ触れます。
ご覧になっていただきありがとうございました。
ご意見などはコメントで。