はじめに

空気や水といった流体のシミュレーションに関する学問である数値流体力学(CFD)の勉強も兼ねて、水の数値流体解析コードの構築に必要な知識などを(複数の記事で)まとめていきたいと思います。

数値流体力学は結構とっつきづらい学問な気がするで、できるだけ初学者にもわかりやすいように書いていきたいと思います。間違い等多々含まれていると思われますので、発見された際にはご連絡していただいけると幸いでございます。また、どこがわかりにくいとかをコメントして頂けたらありがたいです。随時更新していきます。

対象読者

Pythonを使える人
数値計算に興味がある人
流体力学に興味がある人
基本的な大学物理や数学を理解している人(微分方程式くらい？)

行列計算に興味がある人

まとめ目次

1章：【Python】流体シミュレーション：移流方程式を実装する
2章：この記事

本記事の大まかな内容

水のシミュレーションで必要な流体の基礎方程式を扱う前段階として、拡散方程式について簡単にまとめて実装も行います。
前回記事を読まなくても理解できるようにしてあります(希望)

記事内目次
拡散方程式
- 拡散数による安定性判定
- 計算条件
実装
1. 中心差分
2. クランクニコルソンの陰解法
まとめ
参考文献

拡散方程式(場の一様化を表す式)

一次元拡散方程式とは

\frac{\partial T}{\partial t} = κ \frac{\partial^{2} T}{\partial x^{2}}

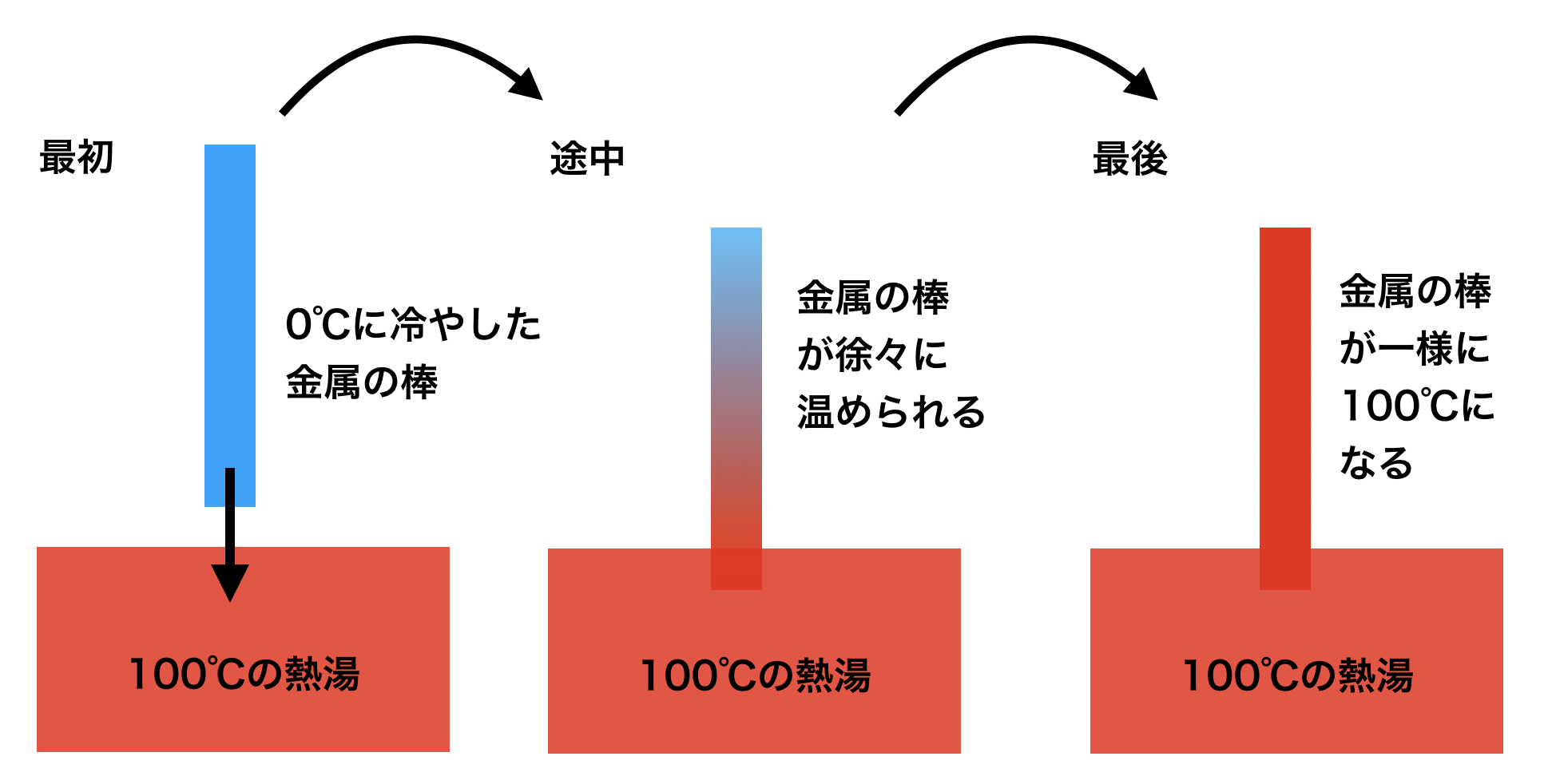
という式で表されます。物理的な意味としては、物理量が無秩序に一様化することを表しています。熱伝導や、熱だけでなく物質の拡散などを意味します。例えば、コーヒーにミルクを入れた場合、かき混ぜなくてもじわっと広がる現象や、以下の図のように金属製の棒の端を沸騰している鍋の中に入れたらじわじわと棒全体がお湯と同じ温度になる現象などが拡散に相当します。

熱拡散の例
- 上の一次元拡散方程式は、下の図のような状況の時の金属棒の温度分布を予測する式です。
- 式中の $κ$ によって、温度の伝わる速度が変化します。大きければ大きいほど、棒全体が100℃になるまでの時間が短いです。

この一次元拡散方程式を離散化する手法としては、陽解法である中心差分法と陰解法のクランク・ニコルソンの陰解法などがあります。おさらいになりますが、陽解法は現在時刻の既知の値をベースに一時刻後の未来の値を予測し、陰解法は一時刻後の未来の値も用いてその値を予測することです。この二つを実装していきます。それぞれを差分式で書き下すと以下のようになります。

中心差分
　　前回の記事で説明した一次精度風上差分を二回行うと導出できます。現在時刻nのデータのみで次の時刻n+1の値を予測する陽解法の一種です。

$\frac{T_{j}^{n + 1} - T_{j}^{n}}{Δ t} = κ \frac{T_{j + 1}^{n} - 2 T_{j}^{n} + T_{j - 1}^{n}}{Δ x^{2}}$
クランク・ニコルソンの陰解法

空間微分に関する偏微分を既知の値(時刻n)と1ステップ後の未知の値(時刻n+1)の平均とする手法。名前にも入っている通り、次の時刻n+1の値を予測するのに次の時刻n+1の値も用いる陰解法です。詳細は後述する。

$\frac{T_{j}^{n + 1} - T_{j}^{n}}{Δ t} = \frac{κ}{2} (\frac{T_{j + 1}^{n} - 2 T_{j}^{n} + T_{j - 1}^{n}}{Δ x^{2}} + \frac{T_{j + 1}^{n + 1} - 2 T_{j}^{n + 1} + T_{j - 1}^{n + 1}}{Δ x^{2}})$

拡散数による安定性の判別

上記で示した離散化手法のうち、中心差分を用いた陽解法に関して、

d = κ \frac{Δ t}{Δ x^{2}}

という拡散数dと呼ばれるものを用いて、数値計算の安定性を判別する必要があります。一方、陰解法に関しては無条件で安定します。

具体的には、

d \leq \frac{1}{2} o r Δ t \leq \frac{(Δ x)^{2}}{2 κ}

の範囲に収める必要があります。この拡散数の条件で大切なのが、刻み幅 $Δ x$ を小さくする場合、時間刻み幅 $Δ t$ をその2乗で小さくしなければならないことです。例えば、

Δ x

を1/2倍したら、

Δ t

を1/4にしなければなりません。これにより、拡散方程式を陽解法で解くのは計算負荷が高くなりがちなので、一般的に陰解法を用いることが多いです。

また、この条件はVon Neumannの安定性解析から求めるのですが、ここでは解説せず直感的なイメージのみ述べておきます。

中心差分の式を書き直すと、

T_{j}^{n + 1} = d T_{j + 1}^{n} + (1 - 2 d) T_{j}^{n} + d T_{j - 1}^{n}

となります。拡散というのは無秩序に一様化することを表すので、

T_{j}^{n}

の係数

(1 - 2 d)

がマイナスになると、j番目の格子が持っている物理量以上を隣に受け渡していることになるため、

d \leq 0.5

である必要があります。

わかりにくいと思うので、下記のお金の例で説明します(あくまでイメージを持つための例です)。N人のグループがあるとして、ある時刻nにj-1番目の人が30円、j番目の人が100円、そしてj+1番目の人が50円持っていることとします。拡散というのはこのN人の人たちが同じ金額を持つようにする操作(一様化)なので、同じ金額になるまで隣の人たちとある一定の割合のお金を交換し続けます。中心差分の式をよく見ると、この一定の割合が拡散数dです。そのため、d=0.1に設定して計算すると、1時刻後のn+1時刻にはj番目の人は88円を持っていることになります。このように考えると、拡散数dが1/2より大きい数を有してはいけないことが簡単にわかると思います。

※拡散の雰囲気を掴むための例です

計算条件

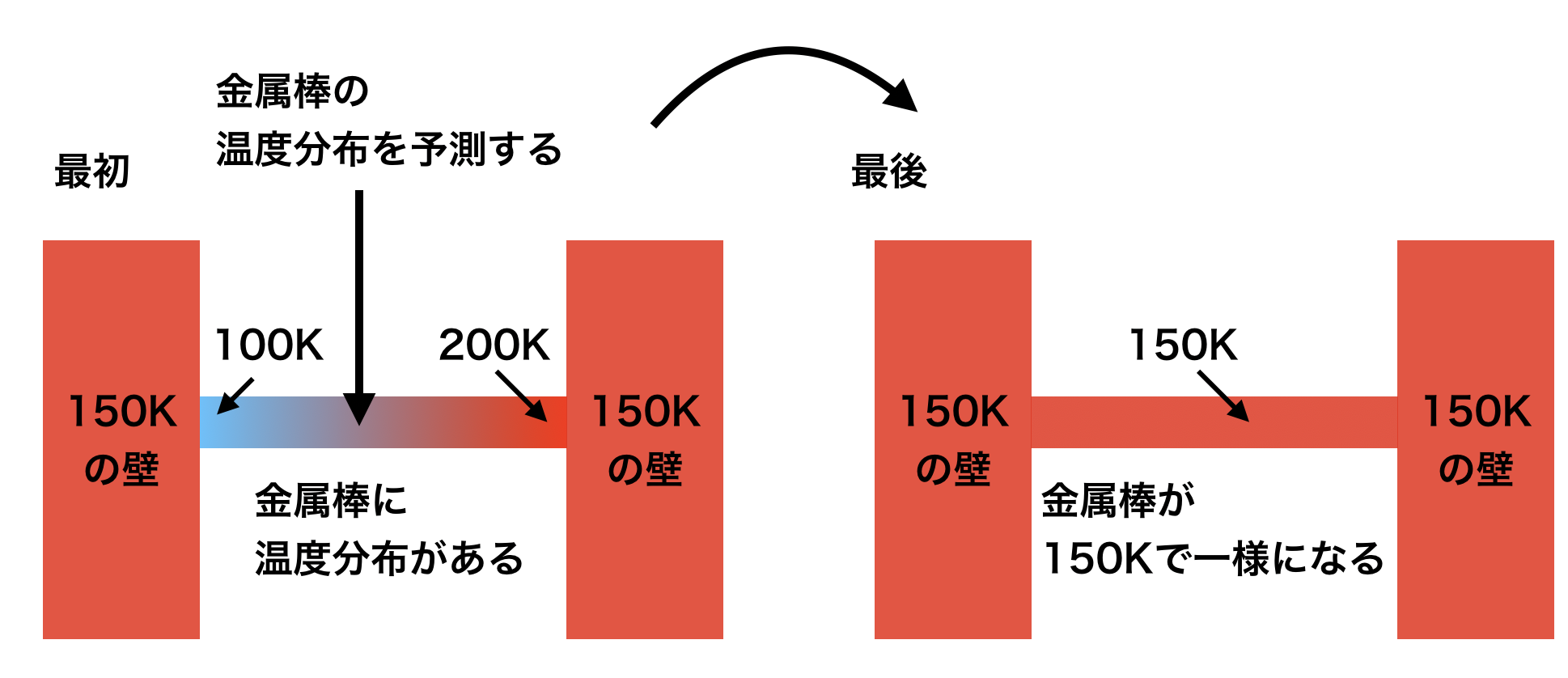
問題
- 100Kから200Kの温度勾配がついている物質(金属とか)を考えて、両端に150Kの熱源を当てたときの温度変化を計算する。簡単に予想できるように、十分に時間が経てば物質全体が150Kで一定になります。変化の途中の温度分布を一次元熱拡散方程式を用いて予測してみます。(補足：Kはケルビンという温度の単位で、273.15K=0℃に相当します)

格子幅 $Δ x$ 、熱伝導係数 $κ$ 、時間刻み幅 $Δ t$ は全て定数として計算する。今回は、 $Δ x = 1$ , $Δ t = 0.2$ , $κ = 0.5$ とし、拡散数 $d = 0.1$ で安定条件下で計算する。

import numpy as np
import matplotlib.pyplot as plt
Num_stencil_x = 101
x_array = np.float64(np.arange(Num_stencil_x))
temperature_array = x_array + 100
temperature_lower_boundary = 150
temperature_upper_boundary = 150
Time_step = 100
Delta_x = max(x_array) / (Num_stencil_x-1)
Delta_t = 0.2
kappa = 0.5
d = kappa * Delta_t / Delta_x**2
exact_temperature_array = (temperature_upper_boundary - temperature_lower_boundary) / (x_array[-1] - x_array[0]) * x_array + temperature_lower_boundary
plt.plot(x_array, temperature_array, label="Initial condition")
plt.plot(x_array, exact_temperature_array, label="Answer", c="black")
plt.legend(loc="lower right")
plt.xlabel("x")
plt.ylabel("Temperature [K]")
plt.xlim(0, max(x_array))
plt.ylim(100, 200)

実装

1. 中心差分

\frac{T_{j}^{n + 1} - T_{j}^{n}}{Δ t} = κ \frac{T_{j + 1}^{n} - 2 T_{j}^{n} + T_{j - 1}^{n}}{Δ x^{2}}

下図は拡散数dが0.1の時の結果です。いくつかのタイムステップ(時刻)に分けてグラフを出力してみました。100時刻後には両端がほぼ150Kに達しており、それに引きずられて温度分布がサインカーブみたいになってます。5000時刻後には、棒全体の温度が150Kに漸近しており中心差分の実装がうまくいっていることがわかります。
実装は式を追いやすいので、numpyの関数をできる限り使わずに書いていきます。

ちなみに、 $κ = 5$ にして拡散数 $d = 1$ で計算すると、下図のように計算が発散して解が求まらないことがわかる。

temperature_explicit = temperature_array.copy()
for n in range(Time_step):
    temperature_old = temperature_explicit.copy()
    temperature_explicit[0] += kappa * Delta_t / Delta_x**2 * \
        (temperature_explicit[1] - 2*temperature_old[0] + temperature_lower_boundary)
    temperature_explicit[-1] += kappa * Delta_t / Delta_x**2 * \
        (temperature_upper_boundary - 2*temperature_old[-1] + temperature_old[-2])
    for j in range(1, Num_stencil_x-1):
        temperature_explicit[j] += kappa * Delta_t / Delta_x**2 * \
            (temperature_old[j+1] - 2*temperature_old[j] + temperature_old[j-1])
plt.plot(x_array, exact_temperature_array, label="Answer", c="black")
plt.plot(x_array, temperature_explicit, label="Explicit(100 steps)")
plt.legend(loc="lower right")
plt.xlabel("x")
plt.ylabel("temperature")
plt.xlim(0, max(x_array))
plt.ylim(100, 200)

2. クランク・ニコルソンの陰解法

\frac{T_{j}^{n + 1} - T_{j}^{n}}{Δ t} = \frac{κ}{2} (\frac{T_{j + 1}^{n} - 2 T_{j}^{n} + T_{j - 1}^{n}}{Δ x^{2}} + \frac{T_{j + 1}^{n + 1} - 2 T_{j}^{n + 1} + T_{j - 1}^{n + 1}}{Δ x^{2}})

これを変形して、時刻n+1の値を左辺に持ってくると

- T_{j + 1}^{n + 1} + 2 (\frac{1}{d} + 1) T_{j}^{n + 1} - T_{j - 1}^{n + 1} = T_{j + 1}^{n} + 2 (\frac{1}{d} - 1) T_{j}^{n} + T_{j - 1}^{n} d = κ \frac{Δ t}{Δ x^{2}}

格子点が1~Mまでの範囲で存在するとして、境界値を $T_{0}, T_{M + 1}$ で表し、行列表示に直すと

(\begin{array}{cccc} 2 (\frac{1}{d} + 1) & - 1 & 0 & \dots & \dots & 0 \\ - 1 & 2 (\frac{1}{d} + 1) & - 1 & 0 & \dots & 0 \\ 0 & - 1 & 2 (\frac{1}{d} + 1) & - 1 & 0 & \dots \\ ⋮ & ⋱ & ⋱ & ⋱ & ⋱ & ⋱ \\ 0 & 0 & ⋱ & - 1 & 2 (\frac{1}{d} + 1) & - 1 \\ 0 & 0 & \dots & 0 & - 1 & 2 (\frac{1}{d} + 1) \end{array}) (\begin{matrix} T_{1}^{n + 1} \\ T_{2}^{n + 1} \\ T_{3}^{n + 1} \\ ⋮ \\ T_{M - 1}^{n + 1} \\ T_{M}^{n + 1} \end{matrix})

= (\begin{matrix} T_{2}^{n} + 2 (\frac{1}{d} - 1) T_{1}^{n} + (T_{0}^{n} + T_{0}^{n + 1}) \\ T_{3}^{n} + 2 (\frac{1}{d} - 1) T_{2}^{n} + T_{1}^{n} \\ T_{4}^{n} + 2 (\frac{1}{d} - 1) T_{3}^{n} + T_{2}^{n} \\ ⋮ \\ T_{M}^{n} + 2 (\frac{1}{d} - 1) T_{M - 1}^{n} + T_{M - 2}^{n} \\ (T_{M + 1}^{n} + T_{M + 1}^{n + 1}) + 2 (\frac{1}{d} - 1) T_{M}^{n} + T_{M - 1}^{n} \end{matrix})

この連立一次元方程式を解くことを考える。格子点数Mが小さい時は未知数が小さいので、筆算のように計算するガウスの直接法と呼ばれる手法など直接的に解を持とめる直接法を用いることができるのですが、Mが大きくなればなるほど計算量的に解を求めることが難しくなる欠点を持ちます。そのため、一般的に大規模連立一次元方程式を解くためには、近似解を厳密解に収束させる反復法と呼ばれる手法が用いられます。

2-1. 直接法

種類は以下の通りです。必要になったら説明します。

ガウスの消去法
- 大学の線形代数の授業で習う掃き出し法と考え方は同じです。
LU分解
コレスキー分解
- コレスキー分解(Cholesky decomposition)
- 修正コレスキー分解(Modified Cholosky decomposition)
- 不完全コレスキー分解(Incomplete Cholosky decomposition : IC法)

2-2. 反復法

A x = b

という一次元連立方程式を解くことを考える。
これを

r = b - A x^{'}

という形に変形し、rが十分小さくなるまで推定値

x^{'}

を反復的に変化させていき、厳密解

x^{*} = A^{- 1} b

の近似解を求める手法が反復法です。反復法は定常法と非定常法(Krylov部分空間法)の二つに分けることができます。

2-2-1. 定常反復法

定常法(定常反復法)とは、反復計算中解ベクトルx以外は変化しない手法のことです。概して遅いので、数値計算をする際には後述する非定常法を用いるか、非定常法の前処理(おおよその近似解を見つけるために行う処理)として併用するかのどっちかの方法をとると思います。

代表的な手法としては以下の３つが挙げられる。以下では、m回の反復における解の推定値を $x^{(m)}$ として表すこととし、m反復目の推定値 $x^{(m)}$ が既知としてm+1反復目の推定値 $x^{(m + 1)}$ を求める計算例を示します。

Jacobi(ヤコビ)法

m+1反復目のi行目の推定解 $x_{i}^{(m + 1)}$ を求める際に、既知の推定解 $x_{i}^{(m)}$ のみを用いて計算する手法。

$x_{i}^{(m + 1)} = \frac{1}{a_{i i}} (b_{i} - \sum_{j = 1, j \neq i}^{n} a_{i j} x_{j}^{(m)})$
Gauss-Seidel(ガウス・ザイデル)法

m+1反復目のi行目の推定解 $x_{i}^{(m + 1)}$ を求める際に、既知の推定解 $x_{i}^{(m)}$ と既に計算されているm+1反復目の推定解 $x_{0}^{(m + 1)}, \dots, x_{i - 1}^{(m + 1)}$ を用いて計算する手法。基本的にヤコビ法よりも収束計算が早く終わる。

$x_{i}^{(m + 1)} = \frac{1}{a_{i i}} (b_{i} - \sum_{j = 1}^{i - 1} a_{i j} x_{j}^{(m + 1)} - \sum_{j = i + 1}^{n} a_{i j} x_{j}^{(m)})$
SOR(Successive Over-Relaxation)法 / 逐次加速緩和法

Gauss-Seidel法に緩和係数 $ω$ を加えたもの。緩和係数 $ω = 1$ のときはガウス・ザイデル法になります。また、1以下だとガウス・ザイデルより収束が遅いが、ガウス・ザイデル法では解けないような問題も解ける。基本的には、1以上の値に設定するが、あまりに大きくしすぎると発散するので適切な値を選ぶのが大切。1.9とかが選ばれることが多いらしい。

$x_{i}^{(m + 1)} = x_{i}^{(m)} + ω \frac{1}{a_{i i}} (b_{i} - \sum_{j = 1}^{i - 1} a_{i j} x_{j}^{(m + 1)} - \sum_{j = i}^{n} a_{i j} x_{j}^{(m)})$
マルチグリッド法
幾何学的マルチグリッド法と代数的マルチグリッド(Algebric Multi-Grid : AMG)法があります。後者のAMG法が非定常法の前処理として使われることが多いです。初めて知る方が多いと思うので詳細は別記事に書きます。

前者3つの項目については、詳細を後述します。

2-2-2. 非定常反復法(Krylov部分空間法)

直接法と反復法の良いとこどりみたいなやつ？反復法に分類されます。

非定常法で最も有名なのが、共役勾配法(Conjugate Gradient method : CG法)です。詳しい説明は、この記事に譲ります。図があってめちゃくちゃわかりやすいです。また、機械学習でよく用いられている最急降下法との違いに関してはこの記事で説明してます。CG法のイメージも書かれていてわかりやすいです。

対称行列
1. 共役勾配法(Conjugate Gradient method : CG法)
2. 前処理付き共役勾配法(Preconditioned Conjugate Gradient method : PCG法)
  1. 不完全コレスキー分解付き共役勾配法(Incomplete Cholesky Conjugate Gradient method : ICCG法)
  2. 不完全LU分解付き共役勾配法(Incomplete LU Conjugate Gradient method : ILUCG)
  3. その他
非対称行列
1. 双共役勾配法(Bi-Conjugate Gradient: BiCG法)
2. 自乗共役勾配法(Conjugate Residual Squared: CGS法)
3. 双共役勾配安定化法(BiCG Stabilization: BiCGSTAB法)
4. 一般化共役残差法(Generalized Conjugate Residual: GCR法)
5. 一般化最小残差法(Generalized Minimal Residual: GMRES法)

こうした手法は、基本的にライブラリとして提供されています。また、計算コードもGithubとかにたくさんあると思います。より詳しく勉強したい方はそちらも参照してみてください。別記事にて、非定常法についてはできる限り多くの手法を説明し、実装もしてみたいと思います。

とりあえずこの記事では、ここまでで説明したアルゴリズムのうち定常反復法のJacobi法・Gauss-Seidel法・SOR法を用いて計算を行なっていきたいと思います。

2-3. 定常反復法の実装

実装は東京大学の中島先生が挙げてくださった資料を参考に実装していきます。説明がわかりにくいと感じましたら、そちらをご参照していただけると幸いです。

以下の例では、

A = (\begin{array}{ccc} a_{1, 1} & a_{1, 2} & \dots & a_{1, n} \\ a_{2, 1} & a_{2, 2} & \dots & a_{2, n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{n, 1} & \dots & \dots & a_{n, n} \end{array}) D = (\begin{array}{ccc} a_{1, 1} & 0 & \dots & 0 \\ 0 & a_{2, 2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & \dots & \dots & a_{n, n} \end{array}) L = (\begin{array}{ccc} 0 & 0 & \dots & 0 \\ a_{2, 1} & 0 & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{n, 1} & \dots & \dots & 0 \end{array}) U = (\begin{array}{ccc} 0 & a_{1, 2} & \dots & a_{1, n} \\ 0 & 0 & \dots & a_{2, n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & \dots & \dots & 0 \end{array})

のように行列を定義する。DはAの対角成分のみ、Lは対角成分の下側(Lower side)、Uは対角成分の上側(Upper side)。

2-3-1. Jacobi法

行列Aの対角成分を有する行列Dと上行列Uと下行列Lを用いて、 $A = D + L + U$ とした時、

A x = b (D + L + U) x = b D x = b - (L + U) x x = D^{- 1} (b - (L + U) x)

のように $A x = b$ が変形でき、一番下の式で反復的に近似解を求める手法がJacobi法と呼ばれます。

x_{i}^{(m + 1)} = \frac{1}{a_{i i}} (b_{i} - \sum_{j = 1, j \neq i}^{n} a_{i j} x_{j}^{(m)})

2-3-1-1. 簡単な例

Aを $3 \times 3$ の行列とする

(\begin{array}{ccc} a_{1, 1} & a_{1, 2} & a_{1, 3} \\ a_{2, 1} & a_{2, 2} & a_{2, 3} \\ a_{3, 1} & a_{3, 2} & a_{3, 3} \end{array}) (\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}) = (\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix})

という一次元連立方程式を解くことを考えます。

反復回数を(m)として表すと、1反復後の(m+1)のときの $x^{(m + 1)}$ の値は、

x_{1}^{(m + 1)} = (b_{1} - a_{1, 2} x_{2}^{(m)} - a_{1, 3} x_{3}^{(m)}) / a_{1, 1} x_{2}^{(m + 1)} = (b_{2} - a_{2, 1} x_{1}^{(m)} - a_{2, 3} x_{3}^{(m)}) / a_{2, 2} x_{3}^{(m + 1)} = (b_{3} - a_{3, 1} x_{1}^{(m)} - a_{3, 2} x_{2}^{(m)}) / a_{3, 3}

という形で表すことができます。この式の形から分かるように、 $x^{(m + 1)} = D^{- 1} (b - (L + R) x^{(m)})$ が成り立っていることがわかります。

そして、以下に示すような収束条件を満たすまで上の計算を繰り返すと、厳密解 $x^{*}$ を求めることができます。

\sum_{j = 1}^{n} | \frac{x_{j}^{(m + 1)} - x_{j}^{(m)}}{x_{j}^{(m + 1)}} | = ϵ

ただし、 $ϵ$ は十分に小さい正数とします。

ここで、簡単な問題でJacobi法で練習してみる。

簡単な例題として

(\begin{array}{ccc} 3 & 2 & - 0.5 \\ 1 & 4 & 1 \\ - 1 & 0 & 4 \end{array}) (\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \end{matrix}) = (\begin{matrix} 3 \\ 2 \\ 1 \end{matrix})

を解くことを考える。答えは

(\begin{matrix} 1 \\ 0.125 \\ 0.5 \end{matrix})

これまでと異なり、numpyの関数を多用して実装していく。圧倒的に見やすくなるので。実装は以下の通り。
実際に計算すると、
Solution [1.00000063 0.12499957 0.50000029] Answer [1. 0.125 0.5 ]
という表示が出て答えが求まっていることが確認できる。

def jacobi(a_matrix, b_array, target_residual):
    """
    ヤコビ法
    Ax = b
    A = (D+L+U)とすると
    Dx = b - (L+U)x
    x = D^{-1} (b - (L+U)x)
    ただし、Dは対角行列、L+Uはその残余行列とする。

    Parameters
    ----------
    a_matrix : numpy.float64
        m×nの行列
    b_array : numpy.float64
        m行の行列
    target_residual : numpy.float64
        正の数。目標とする残差。

    Returns
    -------
    x : numpy.float64
        m行の行列
    """
    x = b_array.copy()
    x_old = b_array.copy()

    diag_matrix= np.diag(a_matrix)  # 対角行列
    l_u_matrix = a_matrix - np.diagflat(diag_matrix)  # 残余行列
    count = 0
    while True:
        count += 1
        x = (b_array - np.dot(l_u_matrix, x_old))/diag_matrix
        residual = np.linalg.norm(x - x_old) / np.linalg.norm(x)
        x_old = x
        if residual <= target_residual:
            break
        elif count >= 10000:
            import sys
            print(residual)
            sys.exit()
    return x

A = np.array([[ 3.0,  2.0, -0.5],
              [ 1.0,  4.0,  1.0],
              [-1.0,  0.0,  4.0]])
b = np.array([3.0, 2.0, 1.0])

x = jacobi(A, b, 10**-6)
print("Solution", x)
print("Answer", np.dot(np.linalg.inv(A),b))

2-3-1-2. Jacobi法注意点

行列Aが(狭義行の)対角優位性を満たさなければ、Jacobi法(とGauss・Seidel法)は収束しません。(狭義行の)対角優位性が何かを簡単に述べると、対角成分は同じ行の他の成分の絶対値の和よりも大きいことを言います。上の練習問題で、対角項以外の成分を大きくして遊んでみてください。

| a_{i i} | > \sum_{j = 1, j \neq i}^{n} | a_{i j} |

2-3-1-3. Jacobi法実装

解くべき式を再掲します。

(\begin{array}{cccc} 2 (\frac{1}{d} + 1) & - 1 & 0 & \dots & \dots & 0 \\ - 1 & 2 (\frac{1}{d} + 1) & - 1 & 0 & \dots & 0 \\ 0 & - 1 & 2 (\frac{1}{d} + 1) & - 1 & 0 & \dots \\ ⋮ & ⋱ & ⋱ & ⋱ & ⋱ & ⋱ \\ 0 & 0 & ⋱ & - 1 & 2 (\frac{1}{d} + 1) & - 1 \\ 0 & 0 & \dots & 0 & - 1 & 2 (\frac{1}{d} + 1) \end{array}) (\begin{matrix} T_{1}^{n + 1} \\ T_{2}^{n + 1} \\ T_{3}^{n + 1} \\ ⋮ \\ T_{M - 1}^{n + 1} \\ T_{M}^{n + 1} \end{matrix})

= (\begin{matrix} T_{2}^{n} + 2 (\frac{1}{d} - 1) T_{1}^{n} + (T_{0}^{n} + T_{0}^{n + 1}) \\ T_{3}^{n} + 2 (\frac{1}{d} - 1) T_{2}^{n} + T_{1}^{n} \\ T_{4}^{n} + 2 (\frac{1}{d} - 1) T_{3}^{n} + T_{2}^{n} \\ ⋮ \\ T_{M}^{n} + 2 (\frac{1}{d} - 1) T_{M - 1}^{n} + T_{M - 2}^{n} \\ (T_{M + 1}^{n} + T_{M + 1}^{n + 1}) + 2 (\frac{1}{d} - 1) T_{M}^{n} + T_{M - 1}^{n} \end{matrix})

結果自体は、中心差分とほぼ同じです。拡散数dは0.1です。

中心差分の時と同じように、拡散数dを1にして計算した結果を下図に示します。拡散数dを0.5以上にしても、解がしっかり求まることがわかります。これが陰解法を使用するメリットです。また、物理的な考察もしておくと、拡散数dが上がったことにより、時間刻み幅と空間刻み幅が一定なので熱が伝わる速度が速くなり、拡散数d=0.1の時より速く150Kに収束していることがわかります。

実装例を以下に示します。構文中のjacobi関数は前々項で構築したものです。

temperature_jacobi = temperature_array.copy()
for n in range(Time_step):
    a_matrix = np.identity(len(temperature_jacobi)) * 2 *(1/d+1) \
                - np.eye(len(temperature_jacobi), k=1) \
                - np.eye(len(temperature_jacobi), k=-1)
    temp_temperature_array = np.append(np.append(
                        temperature_lower_boundary, 
                        temperature_jacobi), temperature_upper_boundary)
    b_array = 2 * (1/d - 1) * temperature_jacobi + temp_temperature_array[2:] + temp_temperature_array[:-2]
    b_array[0] += temperature_lower_boundary
    b_array[-1] += temperature_upper_boundary
    temperature_jacobi = jacobi(a_matrix, b_array, 1e-8)
plt.plot(x_array, exact_temperature_array, label="Answer", c="black")
plt.plot(x_array, temperature_jacobi, label="Implicit Jacobi(100 steps)")
plt.legend(loc="lower right")
plt.xlabel("x")
plt.ylabel("temperature")
plt.xlim(0, max(x_array))
plt.ylim(100, 200)

2-3-2. Gauss-Seidel法(ガウス・ザイデル法)

行列Aの対角成分を有する行列Dと上三角行列Uと下三角行列Lを用いて、 $A = D + L + U$ とした時、

A x = b (D + L + U) x = b (D + L) x^{(m + 1)} = b - U x^{(m)} x^{(m + 1)} = D^{- 1} (b - L x^{(m + 1)} - U x^{(m)}) x^{(m + 1)} = (D + L)^{- 1} (b - U x^{(m)})

のように $A x = b$ が変形でき、一番下の式で反復的に近似解を求める手法がGauss-Seidel法と呼ばれます。

x_{i}^{(m + 1)} = \frac{1}{a_{i i}} (b_{i} - \sum_{j = 1}^{i - 1} a_{i j} x_{j}^{(m + 1)} - \sum_{j = i + 1}^{n} a_{i j} x_{j}^{(m)})

2-3-2-1. Gauss-Seidel法注意点

Jacobi法のところで述べたように、係数行列Aが(狭義行の)対角優位性を満たさなければ、Gauss・Seidel法は収束しません。

2-3-2-2. Gauss-Seidel法実装

特にグラフに変化はありません。

def gauss_seidel(a_matrix, b_array, target_residual):
    """
    Gauss-Seidel法
    Ax = b
    A = (D+L+U)とすると
    x^{(m+1)} = D^{-1}(b- L x^{(m+1)} - U x^{(m)})
    x^{(m+1)} = (D+L)^{-1}(b - U x^{(m)})
    ただし、Dは対角行列、Lは下三角行列、Uは上三角行列とする。

    Parameters
    ----------
    a_matrix : numpy.float64
        n×mの行列
    b_array : numpy.float64
        n行の行列
    target_residual : numpy.float64
        正の数。目標とする残差。

    Returns
    -------
    x : numpy.float64
        n行の行列
    """
    x_old = b_array.copy()
    lower_matrix = np.tril(a_matrix) # 下三角行列
    upper_matrix = a_matrix - lower_matrix  # 上三角行列
    inv_lower_matrix = np.linalg.inv(lower_matrix)
    count = 0
    while True:
        count += 1
        x = np.dot(inv_lower_matrix, (b_array - np.dot(upper_matrix, x_old)))
        residual = np.linalg.norm(x - x_old) / np.linalg.norm(x)
        x_old = x
        if residual <= target_residual:
            break
        elif count >= 10000:
            import sys
            print(residual)
            sys.exit()
    return x

temperature_gs = temperature_array.copy()
for n in range(Time_step):
    a_matrix = np.identity(len(temperature_gs)) * 2 *(1/d+1) \
                - np.eye(len(temperature_gs), k=1) \
                - np.eye(len(temperature_gs), k=-1)
    temp_temperature_array = np.append(np.append(
                        temperature_lower_boundary, 
                        temperature_gs), temperature_upper_boundary)
    b_array = 2 * (1/d - 1) * temperature_gs + temp_temperature_array[2:] + temp_temperature_array[:-2]
    b_array[0] += temperature_lower_boundary
    b_array[-1] += temperature_upper_boundary
    temperature_gs = gauss_seidel(a_matrix, b_array, 1e-8)
plt.plot(x_array, exact_temperature_array, label="Answer", c="black")
plt.plot(x_array, temperature_gs, label="Implicit Gauss-Seidel(100 steps)")
plt.legend(loc="lower right")
plt.xlabel("x")
plt.ylabel("temperature")
plt.xlim(0, max(x_array))
plt.ylim(100, 200)

2-3-3. SOR法

ガウスザイデル法に緩和係数 $ω$ を追加したもの。 $ω = 1$ の時、ガウス・ザイデル法と同じ。
行列Aの対角成分を有する行列Dと上行列Uと下行列Lを用いて、 $A = D + L + U$ とした時、

A x = b (D + L + U) x = b {\tilde{x}}^{(m + 1)} = D^{- 1} (b - L x^{(m + 1)} - U x^{(m)}) : G a u s s - S e i d e l x^{(m + 1)} = x^{(m)} + ω ({\tilde{x}}^{(m + 1)} - x^{(m)})

のように $A x = b$ が変形でき、一番下の式で反復的に近似解を求める手法がSOR法(逐次加速緩和法)と呼ばれます。

x_{i}^{(m + 1)} = x_{i}^{(m)} + ω \frac{1}{a_{i i}} (b_{i} - \sum_{j = 1}^{i - 1} a_{i j} x_{j}^{(m + 1)} - \sum_{j = i}^{n} a_{i j} x_{j}^{(m)})

2-3-3-1. SOR法実装

今回、緩和係数 $ω$ は定数とした。緩和係数 $ω$ は、最適値を決定できる場合もあります。グラフに変化はありません。

def sor(a_matrix, b_array, target_residual):
    """
    SOR法
    Ax = b
    A = (D+L+U)とすると
    x~^{(m+1)} = D^{-1}(b- L x^{(m+1)} - U x^{(m)}) : Gauss-Seidel
    x^{(m+1)} = x^{(m)} + omega (x~^{(m+1)} - x^{(m)})
    ただし、Dは対角行列、Lは下三角行列、Uは上三角行列とする。

    Parameters
    ----------
    a_matrix : numpy.float64
        n×mの行列
    b_array : numpy.float64
        n行の行列
    target_residual : numpy.float64
        正の数。目標とする残差。

    Returns
    -------
    x : numpy.float64
        n行の行列
    """
    x_old = b_array.copy()
    lower_matrix = np.tril(a_matrix) # 下三角行列
    upper_matrix = a_matrix - lower_matrix  # 上三角行列
    inv_lower_matrix = np.linalg.inv(lower_matrix)
    omega = 1.9  # 今回の例だと収束が遅いかもしれません。
    count = 0
    while True:
        count += 1
        x_tilde = np.dot(inv_lower_matrix, (b_array - np.dot(upper_matrix, x_old)))
        x = x_old + omega * (x_tilde - x_old)
        residual = np.linalg.norm(x - x_old) / np.linalg.norm(x)
        x_old = x
        if residual <= target_residual:
            break
        elif count >= 10000:
            import sys
            print(residual)
            sys.exit()
    return x

temperature_sor = temperature_array.copy()
for n in range(Time_step):
    a_matrix = np.identity(len(temperature_sor)) * 2 *(1/d+1) \
                - np.eye(len(temperature_sor), k=1) \
                - np.eye(len(temperature_sor), k=-1)
    temp_temperature_array = np.append(np.append(
                        temperature_lower_boundary, 
                        temperature_sor), temperature_upper_boundary)
    b_array = 2 * (1/d - 1) * temperature_sor + temp_temperature_array[2:] + temp_temperature_array[:-2]
    b_array[0] += temperature_lower_boundary
    b_array[-1] += temperature_upper_boundary
    temperature_sor = sor(a_matrix, b_array, 1e-8)
plt.plot(x_array, exact_temperature_array, label="Answer", c="black")
plt.plot(x_array, temperature_sor, label="Implicit SOR(100 steps)")
plt.legend(loc="lower right")
plt.xlabel("x")
plt.ylabel("temperature")
plt.xlim(0, max(x_array))
plt.ylim(100, 200)

まとめ

一次元拡散方程式を、陽解法の中心差分法とクランク・ニコルソンの陰解法で解きました。
一次元拡散方程式の陽解法では、拡散数による格子幅と時間刻み幅の制限が存在することを確認しました。
クランク・ニコルソンの陰解法を実装には、反復法を用いました。
- 反復法には、定常反復法・非定常反復法(Krylov部分空間法)が存在します。
- 今回の実装では、Jacobi法・Gauss-Seidel法・SOR法を用いました。
- 反復法を用いれば、陽解法のような拡散数による制限の影響を受けないことを確認しました。
- 定常反復法のマルチグリッド法や非定常反復法などは次回以降の記事で説明します。

次回は、非定常反復法(Krylov部分空間法)についてまとめたいと思います。

参考文献

https://qiita.com/sci_Haru/items/960687f13962d63b64a0
https://qiita.com/IshitaTakeshi/items/cf106c139660ef138185
http://nkl.cc.u-tokyo.ac.jp/14n/PDE.pdf
https://home.hiroshima-u.ac.jp/nakakuki/other/simusemi-20070907.pdf
https://www.sit.ac.jp/user/konishi/JPN/L_Support/SupportPDF/InplicitMethod.pdf ←めちゃくちゃわかりやすい
http://ri2t.kyushu-u.ac.jp/~watanabe/RESERCH/MANUSCRIPT/KOHO/GEPP/GEPP.pdf ←網羅的で詳しい

反復法参考文献

反復法とかは、東京大学の中島先生が挙げてくださっている資料や動画とか、数値解析についてまとまっているこのサイトを見れば大体わかると思います。中島先生は神です。

Jacobi法参考文献

定常緩和法実装参考文献

http://nkl.cc.u-tokyo.ac.jp/13n/SolverIterative.pdf
https://ja.wikipedia.org/wiki/SOR法
以下三つのWebサイトは、定常緩和法の実装を非常にわかりやすくまとめてくださっております。
https://org-technology.com/posts/solving-linear-equations-yacobi.html
https://org-technology.com/posts/solving-linear-equations-gauss-seidel.html
https://org-technology.com/posts/solving-linear-equations-sor.html

【Python】流体シミュレーション : 拡散方程式を実装する