はじめに
この記事は,森村哲郎『強化学習』講談社 を中心として記載しています.記事内に参考文献の記載がない場合は,こちらの本を参考にしています.本書は数理的にはっきりと書かれていて,論文を読まないと得られなかった情報が詰まっており,非常に素晴らしい本のですが,(私のような)初学習者が読むと,やや見通しが難しいかなと思いました.
そこで,私の復習も兼ねて,自分の言葉で最低限必要なエッセンスをとりまとめようと思い,本記事を書きます.
本記事の趣旨は,「TD学習,Q学習といろいろあるけど違いがよくわからなくて混乱するのを解消しよう!」というものです.すなわち,強化学習手法の見通しを良くするための記事なので,詳細な理論は他の記事や参考文献を一読してください.
前述のように,あくまで私の言葉で(数式は別ですが)記述するのを念頭に置いており,引用の場合はそれを明示しますが,万が一,著作権的に問題がある箇所があれば,ご一報ください.
今回は省略した手法なども随時アップデートできればと考えています.
強化学習とは
機械学習の定番書であるPRML[2]の3ページには以下のように記載されています.
Finally, the technique of reinforcement learning (Sutton and Barto, 1998) is concerned
with the problem of finding suitable actions to take in a given situation in
order to maximize a reward.
すなわち,報酬最大化 を目指すことによって,最適な,もしくは最適に近い意思決定のルールを求めるのが強化学習(Reinforcement Learning)になります.教師付き学習(Supervised Learning)や教師無し学習(Unsupervised Learning)とともに,機械学習(Machine Learning)もしくはパターン認識(Pattern Recognition)と呼ばれる学問分野の一角をなすものです.ベイズ推定的な観点による尤度最大化などを大きな解法としている後者2つとは,やや毛色が異なりますね.
事前準備
ここでは,本記事を読むのに必要な知識事項をまとめたいと思います.
強化学習の基本的概念
基本的な概念は以下のサイトを参考にしてください.
https://deepage.net/machine_learning/2017/08/10/reinforcement-learning.html#強化学習の位置づけ
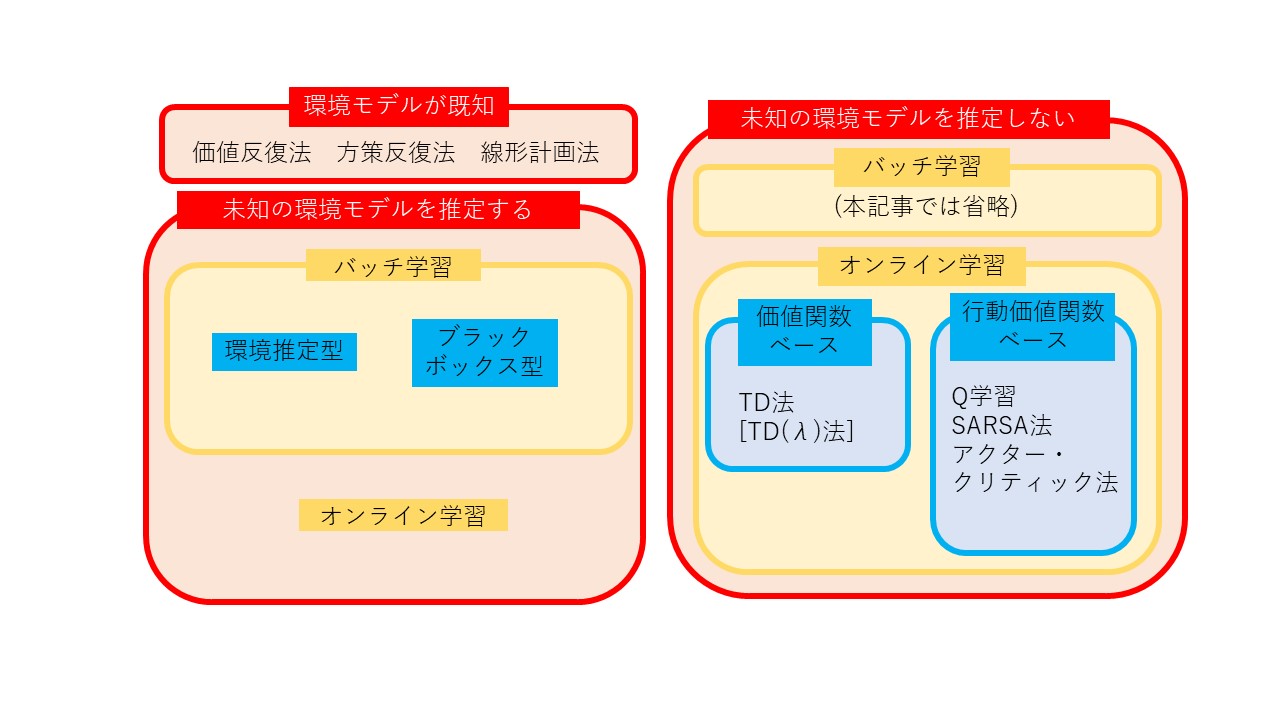
本記事では,
(1) 既知の環境モデル下での強化学習 (価値反復法/方策反復法/線形計画法)
(2) 未知の環境モデルを推定しない強化学習(TD学習/Q学習/SARSA法/アクタークリティック法)
(3) 未知の環境モデルを推定する強化学習
(4) その他発展事項
の4パターンに分類して紹介します.
本記事における文字表記
| 文字 | 意味 | 備考 |
|---|---|---|
| 行動 | ||
| 方策 | ある状態sのときに行動aを選択する | |
| 報酬 | ||
| 状態 | ||
| 価値関数 | ||
| 割引率 | ||
| 学習率 |
また,下付き添え字はある時刻における変数を意味しています.
既知の環境モデル下での強化学習
一般に,この場合は強化学習ではなくプランニングと呼ばれます.
動的計画法1 価値反復法
動的計画法とは,分割統治法の変形です.問題を小さなパーツに分解し,それを記録していき,その組み合わせによって最終的な解を求める,というものです[4].
なお,基本的な動的計画法のプログラミングはこちらがおすすめです.
さて,本題です.強化学習においては,価値関数(あるいは目的関数)を最適化したものを求めることになります.こうして求まった最適価値関数は,行動 によって決まります.そしてこの行動を左右するのが,方策 です.すなわち,最適な価値関数がもとまれば,理論的に方策が求まります.以上の観点から,価値関数を最適にするよう動的計画法を行うのが本手法です.
動的計画法2 方策反復法
前述の価値反復法では,価値関数を逐次的に更新することで,最適な場合をもみつけ,そこから最適方策を求めました.本手法は,価値関数を仲介するのではなく,方策自体を逐次更新して,最適方策を求める手法になります.
線形計画法
前2項目では,動的計画法に基づく手法を紹介しましたが,線形計画法でも求めることは可能です.
すなわち,ある制約条件下で価値関数を最小化するという線形計画問題(主問題)に帰着させるということです(最初に記載した通り,本記事の趣旨上,数式的な詳細は割愛します).
数理最適化を学んだ方はご存じでしょうが,線形計画問題では上記のような主問題とよばれる問題を,双対問題と呼ばれる別の形に変換して考えることが多々あります.そして,これらに対して強双対性が認められる場合は,これらの最適値が一致する,ということが分かっています.例えば,機械学習の分野では,カーネル法+SVMにおいて双対問題は利用されます[2].今回のようなプランニングでも双対問題が利用されることがあります.
未知の環境モデルを推定しない強化学習
(a) 価値関数からの最適化
(b) 方策と行動価値関数からの最適化
の2つに分けて解説します.ここからさらに,バッチ学習型とオンライン学習型のさらに2つに分けられますが,
○○法として良く知られたものをわかりやすく分類する,という本記事の趣旨から,バッチ学習型の手法については触れず,オンライン学習型の手法のみ,すなわち時々刻々とデータが追加されていく中での強化学習手法を紹介します.
価値関数からの最適化
本節では,固定された方策 に従ってエージェントが行動した際の価値関数を推定するということを考えます.前節の「環境モデルが既知の場合」では,価値関数というのは明示的でしたが,今回の「環境モデルが未知の場合」は,価値関数の推定(推定価値関数 )が必要です.
TD(temporal difference)法
本手法では,以下のような値,TD誤差 を利用します.
ここで, は時刻における報酬, は割引率を表します.すなわち,TD誤差は,あるステップとその次のステップにおける推定価値関数の差と報酬の和として定義されます.これを利用して,推定価値関数を適当な初期値からスタートして以下のように逐次更新します.
まず,方策に従って,行動をとり,その結果として,報酬と次の状態を観測します.
そして次の式で推定価値関数を更新します.
は学習率です.t=t+1としながら,何らかの終了条件(最大ステップ数など)まで繰り返します.
方策と行動価値関数からの最適化
前節では,状態に着目して価値関数の推定を考えましたが,本節では行動も含めて考えましょう.
Q学習
価値関数 は状態 の関数()でしたが,ここでは補助変数として,新たに行動価値関数 を導入します.Qは状態だけでなく,行動 によっても値が変わります.すなわち という2変数の関数ということになります.具体的には,以下の関係式で結びつきます.
ここではすべての行動の集合で,ハットは「推定」であることを表します.前述の通り,「環境が未知」なので,推定する他ないのです.あとは,Q学習とほぼ同じです.方策 に従って,行動をとり,その結果として,報酬と次の状態を観測します.そして以下のようにして,推定行動価値関数を更新していきます.
SARSA法
ほとんどQ学習と同じです.学習の式を見てみましょう.
どこが違うのかというと,1つ目の式の右辺2項目です.Q学習では,とりうる行動から最も の高くなる行動を選ぶということになっています.しかし,SARSA法では,となっています.前者の場合,ある定まった方策に関して,を用いて評価します(方策評価).一方,後者の場合は,評価するだけでなく方策自体も更新されていきます(方策改善).前者のような手法を方策オフ型,後者のような手法を方策オン型と呼びます.Q学習とSARSAの違いは[3]にまとまっています.
アクター・クリティック法
アクター・クリティック法は,SARSA法と似ており,方策オン型の手法です.SARSA法では,という単一の指標を用いて方策評価と方策改善を行いました.これを分離させたものが本手法であると直感的には捉えられます.
アクター(方策)とクリティック(方策評価)という2つのモジュールを用意し,クリティックが方策改善信号をアクターに送り,アクターはそれによって方策を更新する,というプロセスです.こういった方針のアルゴリズムによって成り立つ手法を総称してアクター・クリティック法と呼んでいます.
未知の環境モデルを推定する強化学習
(a) バッチ学習-環境推定型
(b) バッチ学習-ブラックボックス型
(c) オンライン学習型
バッチ学習-環境推定型
環境を何らかの形で明確なモデルとして推定し,前述のプランニング手法を適用して学習しますます.このモデルの推定方法は,最も簡易的には,[状態・行動・次状態]のセットデータから,状態遷移確率や報酬を最尤推定推定するという方法があります.
また,発展的な手法として,ベイジアン強化学習,逆強化学習,模倣学習なども存在します.
バッチ学習-ブラックボックス型
ここでいうブラックボックスとは,「行動と状態」から「報酬と次状態」を吐き出すような生成モデルを指しています.様々な時系列入力に対して,様々な出力が出てきますが,それは木構造で表現されます.この木探索をすることが,プランニングになります.
具体的には,スパースサンプリング法,モンテカルロ木探索などがあります.
オンライン学習型
環境モデルを明らかにしない場合のオンライン学習則,すなわちTD法やSARSA法などは,行動によって決まった次の状態や報酬をもとに,価値関数や方策を考えていました.モデルを推定する場合は,これに並行して,マルコフ決定過程的な環境モデルを推定することになります.この際,
①環境の不確実性を下げる行動を取って環境モデルを精緻化するか(今までやってこなかった行動をするなど),
②目的関数の最大化をするか
というトレードオフが重要になります(もちろん,方策と探索のトレードオフは環境モデルを推定しない場合にも非常に重要です).
具体的には,R-max法,E3法などがあります.
その他発展事項
ここでは,より発展的な手法を名前だけ紹介します.
必要に応じて,論文や参考文献[1]を参照してください.
関数近似手法
ここまでの手法では,必要なメモリが多いなどいくつかの問題があるため,代わりとして以下の
手法が存在します.
・価値関数の近似
・テーブルの拡張による解決
・適合価値反復法 ・適合Q反復法
・ニューラル適合Q反復法 ・DQN
・近似TD法 ・近似Q学習 ・近似SARSA法
・損失関数の利用
・最小二乗法アプローチ
最小二乗TD法(LSTD)・逐次LSTD法・最小二乗方策反復法
・勾配降下法の利用
勾配TD法・勾配Q学習
参考文献
[1] 森村哲郎『強化学習』講談社
[2] C. M. Bishop "Pattern Recognition and Machine Learning" Springer
[3] http://cookie-box.hatenablog.com/entry/2016/04/17/120548
[4] G. T. Heineman 他 『アルゴリズム クイックリファレンス 第2版』オライリー・ジャパン