概要
3Dが絡むプログラムでは「オブジェクトの姿勢を基準に判定したい」とか「マウスの操作を3D空間の操作に変換したい」とか「あるオブジェクトを自動で制御したい」といった気持ちになります。
その気持ちを実現するにはベクトルと回転を理解して、実装する必要があります。
私自身もまだまだ理解は浅いですが、現時点での備忘録として残しておきます。
「このオブジェクトの前」という気持ち
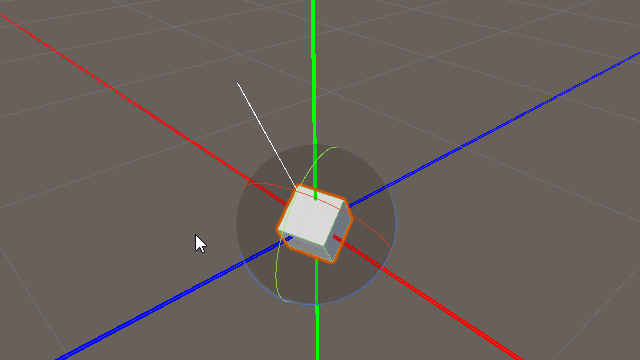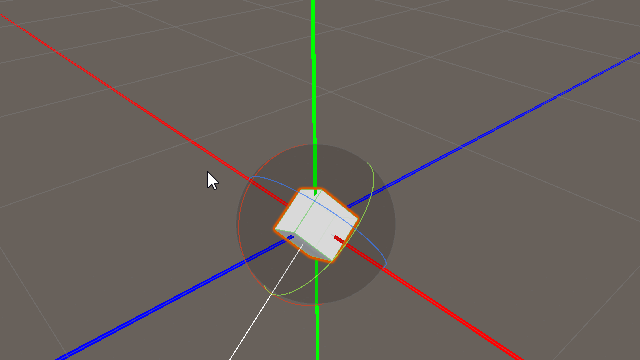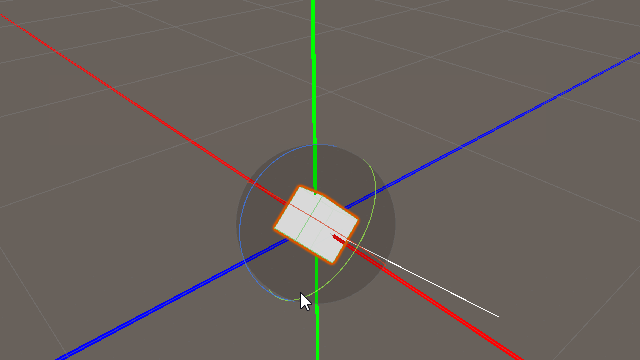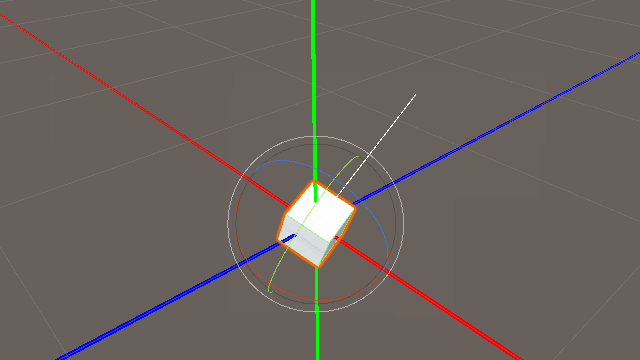
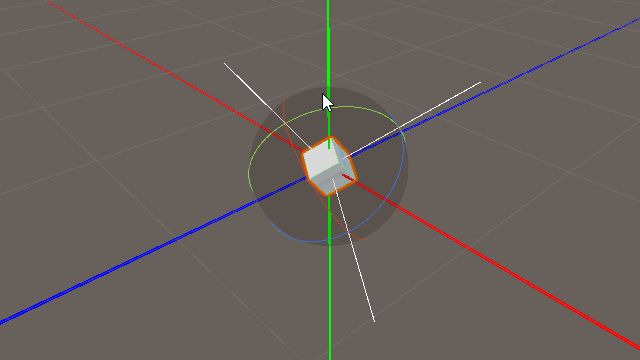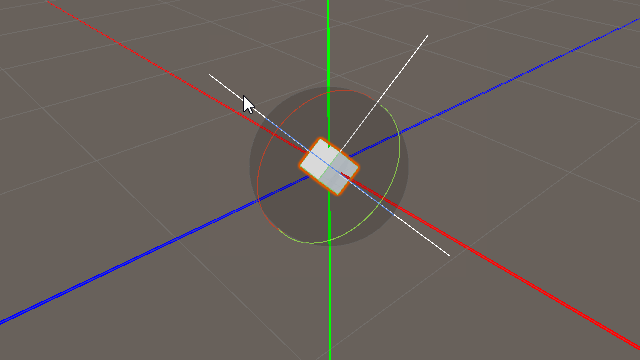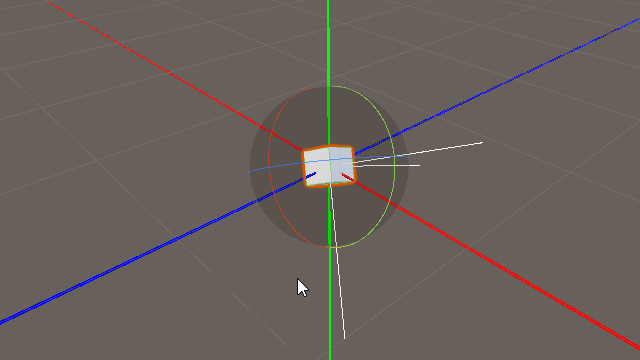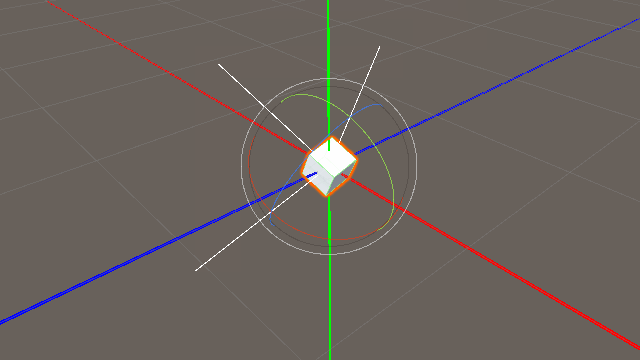
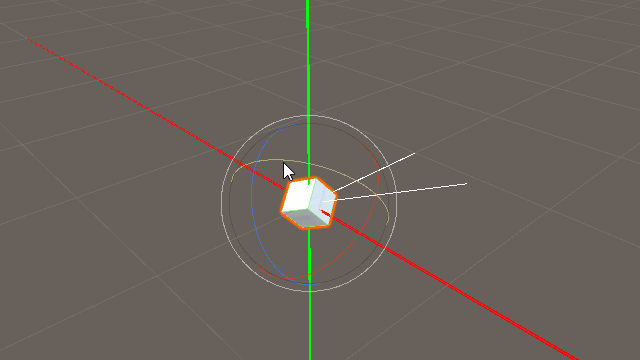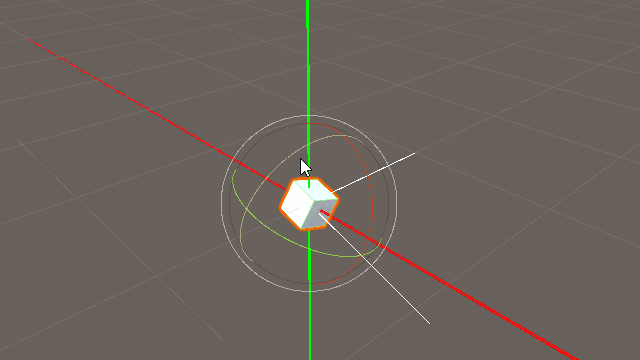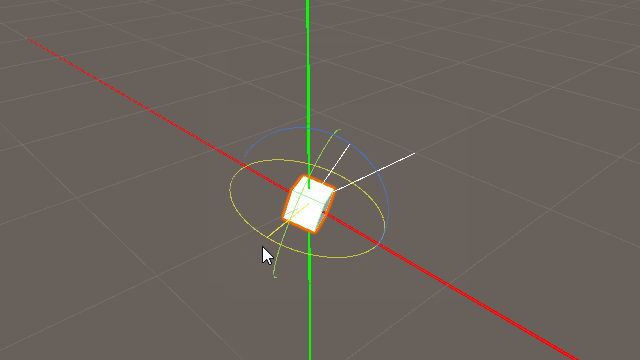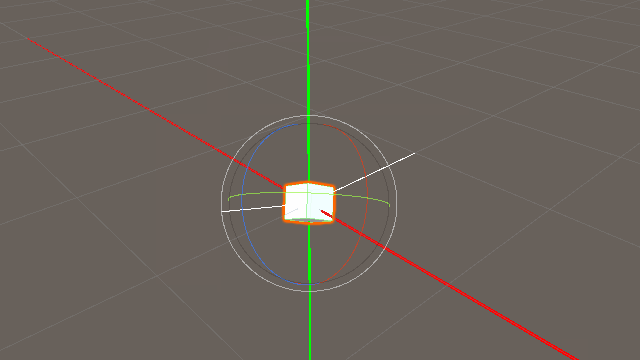
「this.gameObject.transform.forward」の意味は「このオブジェクトを基準にしたZ方向 (0,0,1) の単位ベクトル」
かみ砕いた表現では「このオブジェクトの前」です。
シンプルで基本的なベクトルなだけに、このベクトルから言える事は多く非常に便利です。
例えば Physics.Raycast のにこのベクトルを渡してあげれば「このオブジェクトの前方にある物」を判定する事ができる。
this.gameObject.transform.forwardを使った移動
this.transform.position += this.gameObject.transform.forward * Time.deltaTime;
「補足」
this.transform は「このスクリプトがアタッチされているオブジェクトのtransform」という意味。例えばcubeにアタッチすればそのcubeのtransformを取ってきます。
Time.deltaTime は「1フレームの処理にかかった時間」です。Time.deltaTimeを掛けてやることで実行中のFPSが60なら60分の1、FPS90なら90分の1にできる。つまり「Time.deltaTimeを掛ける=1フレームの変化量にする」と同じ意味である。
「transform.forward」を現在地である「transform.position」に足してやることで「そのオブジェクトは(そのオブジェクトを基準にして)前方に移動する」という気持ちが表現できる。
前に進めるのも、前にあるものが何かわかるのも「このオブジェクトの前 (this.gameObject.transform.forward)」という気持ちが書けるおかげなので「this.gameObject.transform.forward は便利」といえる。
「向きを変える」という気持ち
transform.forward の部分を transform.up transform.right に置き換える事で上下・左右と言い換えることもできます。(反対方向は-をつければよい)
これは transform が使える機能の一部です。
更に掘り下げると forward と up で何が違うのか?という疑問が生まれます。
transform.forward の正体は何なのか?
this.gameObject.transform.rotation * new Vector3(0, 0, 1.0f);
この書き方をしても transform.forward と同じ結果が得られます。
つまり、「this.gameObject.transform.forward」とは、単位ベクトル Vector3(0,0,1.0f) とゲームオブジェクトの持つ回転(クォータニオン)を掛けたものである。
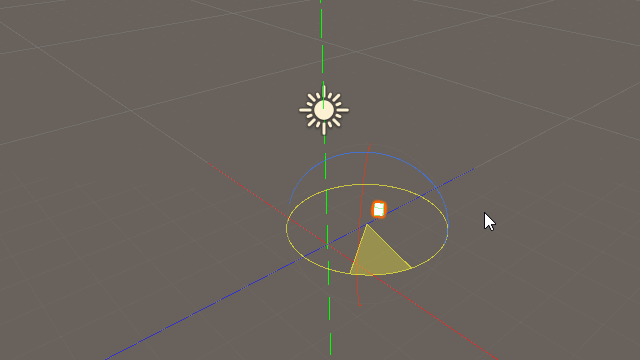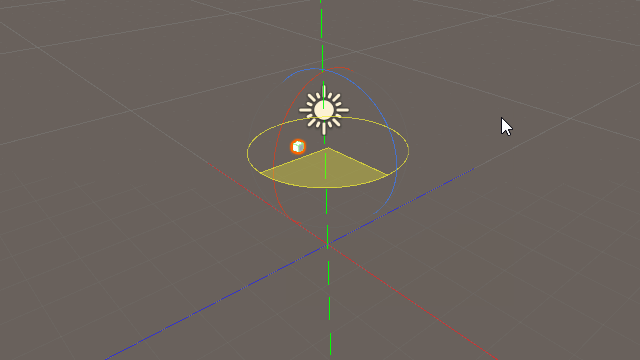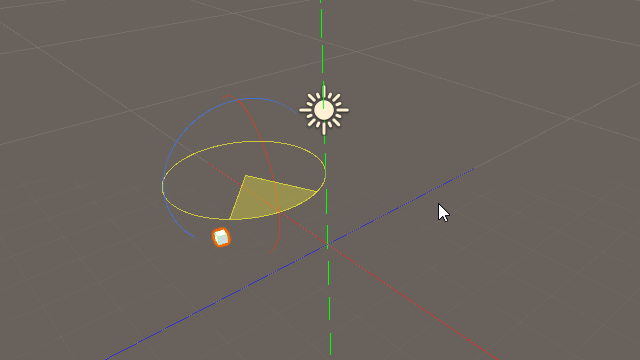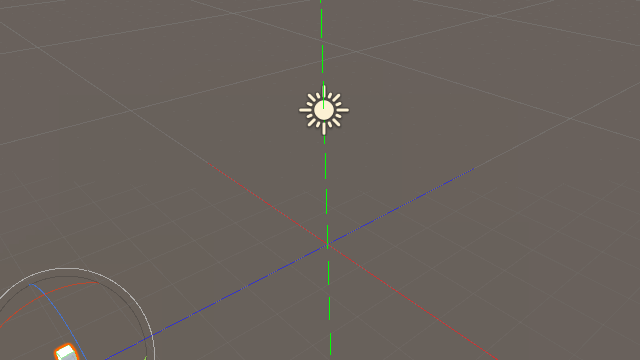
上の図は「transform.forward」と「Vector3(0,0,1.0f)」を比較したものである。
当然ながら、Vector3(0,0,1.0f)は定数なので、ゲームオブジェクトの姿勢を変化させても変化せず常に一定方向である。
「変化しない方向を示したい」という気持ちであれば、このように定数で書けばよいが…多くの場合は「ある基準に対するこの方向を示したい」という事の方が多い。
つまり「ある基準」という気持ちは「this.gameObject.transform.rotation (transform.rotation)」で表現でき「この方向」という気持ちは「単位ベクトル」で表現できる。
その二つを掛けると「ある基準に対するこの方向」という気持ちを表現する事になり…「このオブジェクトを基準としたZ方向」という気持ちを機能として実装しているのが「this.gameObject.transform.forward」である。
クォータニオン、クォータニオンってなんだ?
【Unity道場 博多スペシャル 2017】クォータニオン完全マスター
虚数i…複素数…複素平面…オイラー角…やめろ!!やめるんだ!!!
1つだけ言えるのは「ヒエラルキーに見えるRotation」は「クォータニオン」を理解しやすい「オイラー角」に変換して表示してくれている・・・という事です。
色々考えましたが、そもそも4次元の話を3次元のイメージで理解しようとするのが困難だったり、原理どうこうといより、計算上の都合や、式の持つ性質をうまくつかっているみたいな要素が多いので…上記のクォータニオン完全マスターを見たり、複素平面とか代数や幾何学の教材を読む方がいいと思います。
まとめ
学校で数学をちゃんとやってれば当たり前…という話なんですけど、私の学生時代は効率よく赤点を回避するか?という事をしていたので、学びなおす事になりました。
数学は物理現象が紐づいてないと、その式が示す実体が掴みづらいと感じます。
例えば三角関数1つとっても、いきなり「X = cosθ」と置かれたところでそのルールが本質的に何であるか?みたいな事が分かりづらいと思うんですよね。
(記号が並んでるだけだと、式がどういう気持ちなのか初見ではわからない)
まずは大きな物を簡単に測量したかった…とか、相似の三角形が便利だと気付いた…とか、そういう気持ちが大事。