コーディング面接とSnakeゲームに唯一共通すること

80年代か90年代に生まれた方ならおそらく、「Snake」というゲームのことをご存じでしょう。「ご存じ」とはつまり、Nokia 3310のちっぽけな画面上でたわいもない巨大ヘビを育てるのに膨大な時間を費やしていたのではないかということです。Nokiaの携帯電話について、皆さんは他にどんな特徴を覚えていますか？

バッテリーが長持ちしたことではないでしょうか。
Nokiaはとても”原始的な”携帯電話であったにもかかわらず、バッテリーを使い果たすことなくSnakeゲームで何時間も遊べたのは、どういう訳だったのでしょう？

理由の大部分は、優れた強固なコンポーネントのおかげでした。しかし、貢献度はそれより低く、あまり語られることもありませんが、スライディングウィンドウと呼ばれる手法も長時間のプレイに役立っていたのです。

Snakeだけを扱った記事を1本書きたいのは山々ですが、実は本記事では後者の、魅力では劣るものの大変重要な手法であるスライディングウィンドウについて取り上げ、以下のような疑問に答えていきたいと思います。

• なぜ私たちやプログラマは、スライディングウィンドウが基本的アルゴリズムだと考えているのか。
• なぜスライディングウィンドウがコーディング面接で頻出するのか。
• スライディングウィンドウはSnakeや”実用的な”アプリケーション内でどう使われているのか。
• コーディング面接でよく登場する問題のうち、スライディングウィンドウを用いて（よりうまく）解けるのはどのようなものか。

次の面接のために準備中の方も、面白そうだから読んでいる方も、何か新しいことを学びたい方も、ぜひ読み進めてください。そして、一番関心のあるセクション以外はどうぞ遠慮なく読み飛ばし、ご自身のお考えをコメント欄にお寄せいただくか、本記事をお読みになった印象に応じて拍手マークをクリック（訳注：元記事の機能）していただけましたら幸いです。

注1：Snakeにのみ関心のある方は（その気持ちは分かりますのでご安心を）、本記事の末尾までスクロールしてください。
注2：コーディング面接の準備をしている方は、Prampをご参照ください。受験仲間と組んで行う無料の模擬面接をご用意しています。

それでは始めましょう。

アルゴリズムに基づくプログラミングは複雑ですが、問題を解くために用いられる本質的な原理は限られた数しかありません。その1つがスライディングウィンドウです。

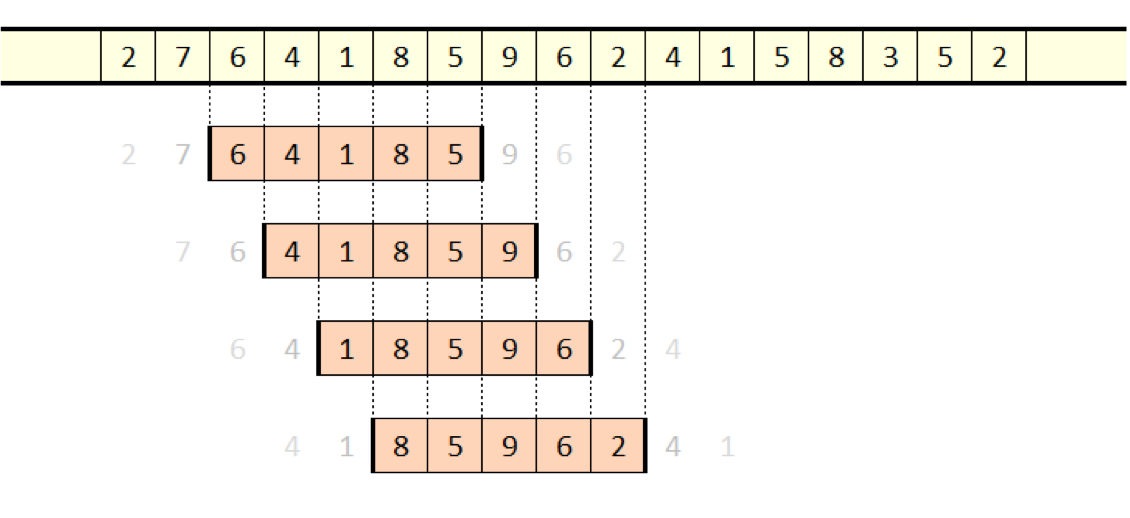
図1：スライディングウィンドウ

ウィンドウ制御のパラダイム

スライディングウィンドウの元となっているより包括的な原理は、ウィンドウ制御です。

ウィンドウ制御では、システム状態の一部に着目しますが、その着目部分のことをウィンドウと呼びます。したがって、ウィンドウ制御アルゴリズムと、ウィンドウを介して明らかになることに適用されるアルゴリズムは、単純に言えば別物です。

システム状態が配列や文字列といったオブジェクトのシーケンスである時は、特殊ケースとなります。ウィンドウを定義するとサブシーケンスが現れるのです。この場合、どんな処理であれ、シーケンス内の他の値は無視してサブシーケンスにさえ適用すればいいわけです。処理する必要のある範囲を限定すると、問題全体を小さくすることができます。スライディングウィンドウの「スライディング」というのは、ウィンドウの位置を1つ右にずらすと、処理を適用できる別のサブシーケンスが出現することを指しています。

以上がこの手法の概要です。アルゴリズムを各ウィンドウに個別に適用する場合は、力ずくの戦術が必要になるでしょう。
しかし、スライディングウィンドウを使えば、ウィンドウをずらす処理そのものを活用してアルゴリズムを再構成することが可能になるのです。その目的はひとえに、より優れた高速なアルゴリズムを構築することです。

少なくとも理論的には、スライディングウィンドウに当てはまるアルゴリズムは、ほぼどんなものでも実行速度を改善することができます。ウィンドウがずれる時、変化する要素は2個だけです。一番古い要素が枠から外れ、一番新しい要素が枠に入ります。

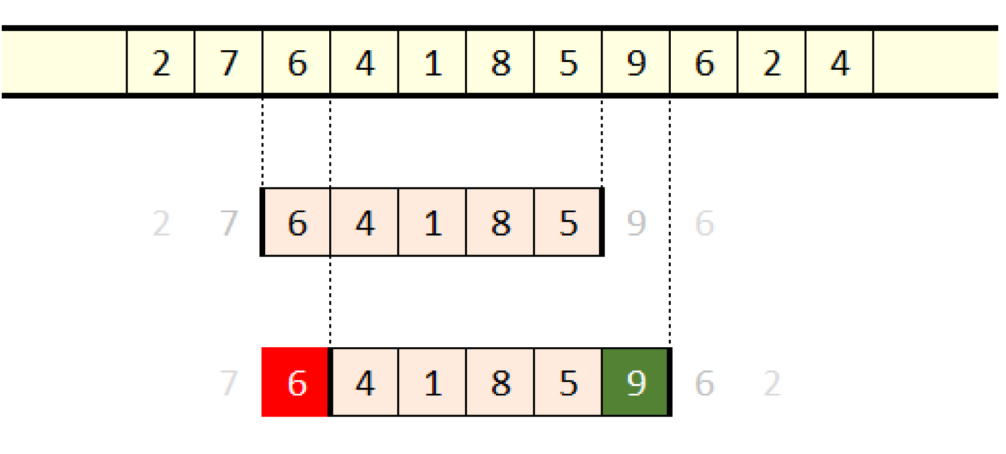
図2：要素のスライディング（赤：外れる、緑：入る）

力ずくでサイズkのウィンドウを1個処理するのにkステップが必要で、シーケンス内にウィンドウがn個あるなら、この力ずくアルゴリズムを完了させるにはn·kステップが必要となります。しかし、ずれるごとに変化する要素は2個だけなので、全実行時間はおよそ2nに比例すると言えます。

シーケンスをたどるだけでO(n)時間がかかるなら、一般的なシーケンスの処理をO(n)より短時間で実行できるアルゴリズムは存在しないことになります。過去の解析からも、「スライディングウィンドウを適切に応用すれば実行時間がO(n)の本格的なシーケンス処理アルゴリズムも作成できる」ということがまさに明らかになっています。

> 言い換えれば、与えられた問題に対してそれ以上速く処理できないような完璧なアルゴリズムを作り出せると約束されているのです。

これで必要な基本情報の説明が終わりましたので、以下では、この一般的なアルゴリズム概念を用いて解くことのできる3つのプログラミング問題を取り上げ、スライディングウィンドウが現実世界のシナリオの中でどのように使われているかの具体例をご紹介したいと思います。

コーディング問題1：移動平均

課題：数列の移動平均を計算するアルゴリズムを作成する。

課題は、与えられた数列a0, a1, … an-1とパラメータk, 0 < k <= nについて、どの要素も「元シーケンスに続くk個の要素の平均」となるような、新しいシーケンスを作ることです。

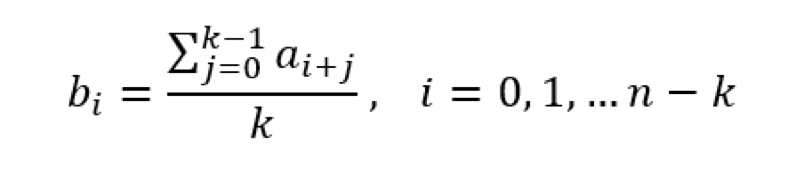
図3：平均の式

背景：移動平均は、入力データストリームを平滑化する際に有用。数値がノイズに影響される場合、生データの傾向が見えにくい。平滑化することで、以下のようなより示唆に富んだ図を得られるようになる。

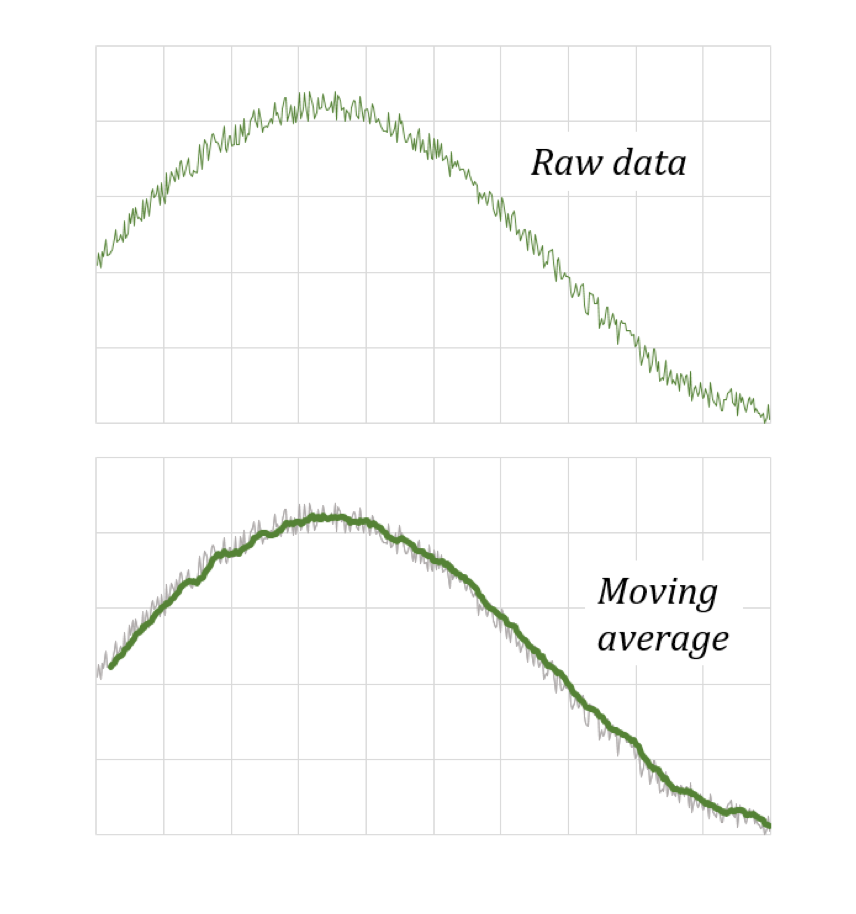
図4：移動平均を取ると入力データを平滑化できる

この問題はスライディングウィンドウを用いると効率的に解くことができます。
すぐに気づくのは、スライディングウィンドウアルゴリズムの大多数に共通する特徴が当てはまる、つまり先頭のk-1個の要素では出力がないということです。最初のウィンドウ全体に空きがなくなった時に初めて、最初の結果が得られます。全ての後続ウィンドウはそれぞれ1個の結果を生み出します。よってスライディングウィンドウアルゴリズムに従う場合、n個の要素を持つシーケンスは、n-k+1個の結果を生むシーケンスを出力します。

それでは実装です。ウィンドウの平均は、全要素の和をウィンドウサイズで割ると得られます。

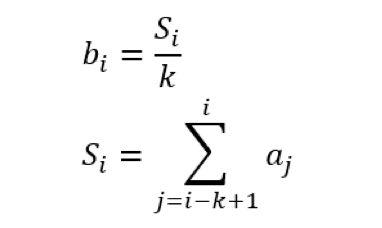
図5：和の式

以上の説明で、スライディングウィンドウを用いる利点がすぐお分かりいただけるでしょう。ウィンドウの和は、直前のウィンドウの和から計算できるのです。

図6：最適化された式

最初のウィンドウでは和の計算にkステップが必要となり、その他全てのウィンドウではさらに2つだけ演算が必要となります。

以下はこの解答をC++で実装したものです。先頭のk個の要素の処理を終えると最初の出力があります。他の出力数値は全て、最適化された総和式で計算されます。

double* moving_average(double* data, int n, int k)
{
assert(data != NULL);
assert(n > 0);
assert(0 < k && k <= n);
double* result = new double[n — k + 1];
double sum = 0;
for (int i = 0; i < k; i++)
{
sum += data[i];
}
result[0] = sum / k;
for (int i = k; i < n; i++)
{
sum = sum — data[i — k] + data[i];
result[i — k + 1] = sum / k;
}
return result;
}

このアルゴリズムで最も重要な点は、元シーケンスのどの要素も多くて2度処理されるということです。よって全体の時間計算量はO(n)となります。

コーディング問題2：和が最大のサブシーケンス

課題：全てのサブシーケンスの中で和が最大になるサブシーケンスを発見するアルゴリズムを作成する。

この問題は、入力データが負の値を取り得る場合には厄介です。

ここでも、スライディングウィンドウを用いて時間計算量がO(n)となる解法を導くことができます。ただし今回は、ウィンドウサイズは固定されません。というよりも、これは最適なウィンドウを見つける問題なので、ウィンドウサイズはウィンドウがずれる過程で変化するのです。

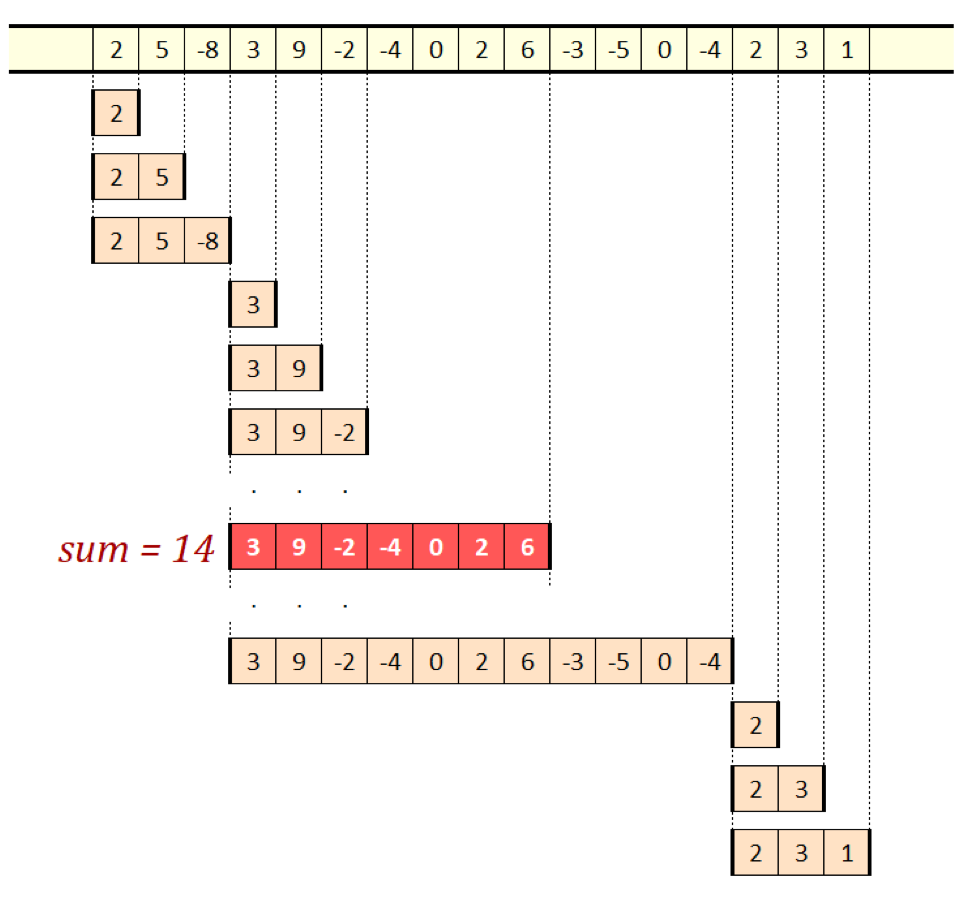
図7：スライディングウィンドウにおける最大の和

考え方としては、すでにウィンドウがある状態で起こることを観察していきますが、ウィンドウの和は分かっています。そして、次に入ってくる値を取り込みたいわけです。この値はウィンドウの和に加算されるかもしれませんし、単位長の新規ウィンドウ全体になるかもしれません。この時調べるのは、どちらのウィンドウの和の方が大きいかということです。どちらにしても、和が大きい方のウィンドウを次のウィンドウとして保持し、次の入力値に移って同じ処理を繰り返します。上の図は、ウィンドウがシーケンスに沿って少しずつずれる様子を示しています。

取るべき選択肢は常に、現在の入力要素の時点で和が最大となるサブシーケンスです。どのウィンドウも、和が負の値になり次第破棄します。その状況では、1個の数値単独の方が、直前の最大のウィンドウ全体に組み込んだ時の和よりも大きいからです。

そうすると、残る唯一のステップは全体の最大値を見つけることです。シーケンスをたどっていく過程で出現した全てのウィンドウが候補となります。シーケンスの終端に到達した時までに生じたウィンドウのうち、和が最大だったウィンドウが、全体の中で和が最大のサブシーケンスということです。

以下は正攻法のC++実装です。やはり、シーケンスのどの要素も多くて2度処理されるので、この関数全体の時間計算量はO(n)となります。

std::tuple<int, int, int> max_sum_subsequence(int* data, int n)
{
assert(data != NULL);
assert(n > 0);
int bestStart = 0;
int bestLength = 1;
int maxSum = data[0];
 
int curStart = bestStart;
int curLength = bestLength;
int curSum = maxSum;
 
for (int i = 1; i < n; i++)
{
if (curSum < 0) { curStart = i; curLength = 1; curSum = data[i]; } else { curLength += 1; curSum += data[i]; } if (curSum > maxSum)
{
bestStart = curStart;
bestLength = curLength;
maxSum = curSum;
}
}
return std::tuple<int, int, int>(bestStart, bestLength, maxSum);
}

コーディング問題3：長さkの各サブシーケンスの最大値

課題：長さnの数値シーケンスにおいて、長さkの各サブシーケンスの最大値を求めるアルゴリズムを作成する。難問なのでご注意を。

このアルゴリズムは画像処理において利用されています。ご想像どおり、O(n)時間で実行できるアルゴリズムが最も重視される分野です。

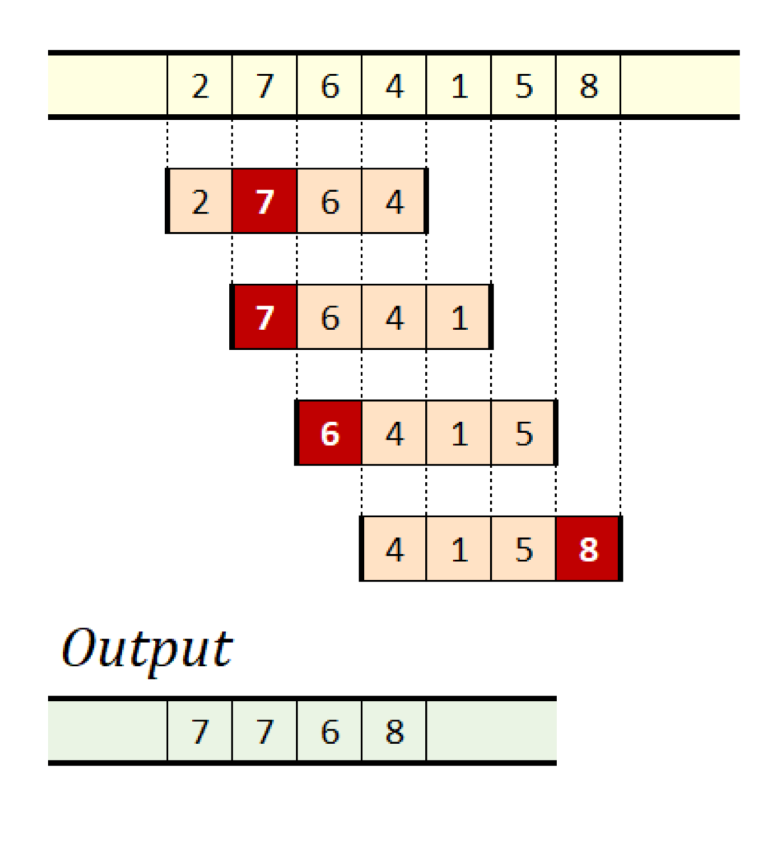
図8：最大値

ウィンドウがずれる時、ウィンドウ内の最大値を出力します。この問題で難しいのは、ウィンドウ内の最大値を求める公式がないことです。そのため、要素の1個を最大値として選ばなくてはなりません。

とはいえ、スライディングウィンドウが役に立たないという意味ではありません。いい方法があります。上図のような4個の値を持つウィンドウの例で考えてみましょう。

枠に新しい値が入ってくる時、既存の値との大小関係を把握する必要があります。1つには、ウィンドウがずれていくにしたがって、全ての既存の値が、この新しい値より先に枠から外れるからです。そこが重要なポイントです。既存の値は、新しい値より小さいなら、枠内にある間はそれより大きな新しい値も必ず枠内にあるわけですから、最大値にはなり得ません。

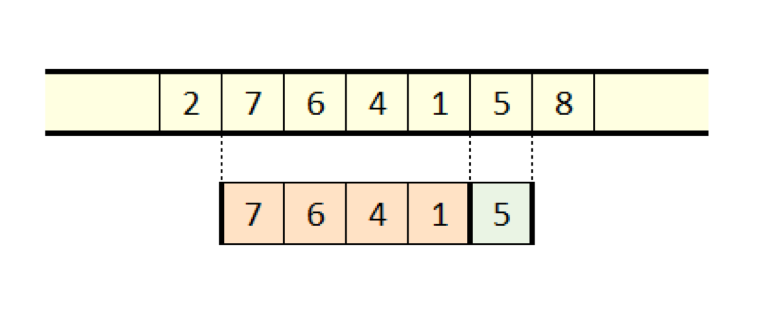
図9：最大値問題におけるスライディング

この考え方でいけば、以下の図にあるように、ウィンドウがずれる度に、ウィンドウ内にある新しい値より小さな値全てを最大値候補から削除することができます。逆に、この動作によって別の結果が生じます。

ウィンドウの右から入ってくる値より小さな値全てを毎回削除するなら、ウィンドウ内には、値が右上がりでなく隣接もしていないサブシーケンスだけが残ります。もう1つの結果として、求めるべき最大値はウィンドウ内の一番左の要素であるということが明らかになります。

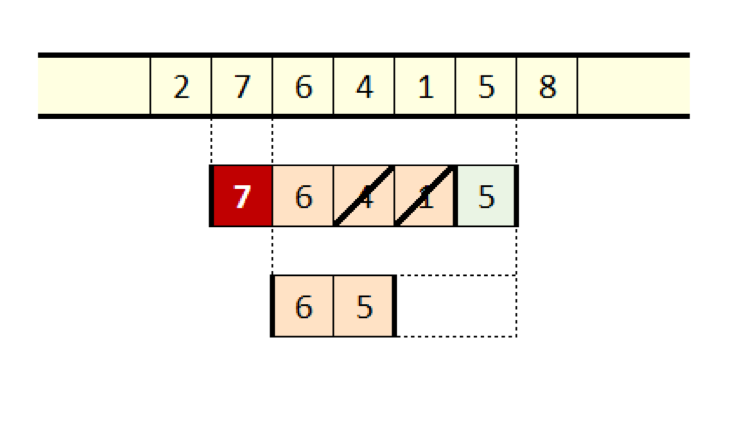
図10：最大値候補からの削除

さらにもう1つ、明確にしておきたいことがあります。ウィンドウがずれると、シーケンスの一番左の値が枠から外れます。この値は、より大きな値が入ってきたためにすでに最大値候補から削除されているかもしれません。あるいは、右から入ってきたどの値よりも大きかったため枠内に残っていたものかもしれません。後者の場合、この値は枠の一番左になって枠から外れるタイミングで削除することになります。

以下の図は、シーケンスの要素が7個でウィンドウサイズが4の場合の過程全体を示したものです。

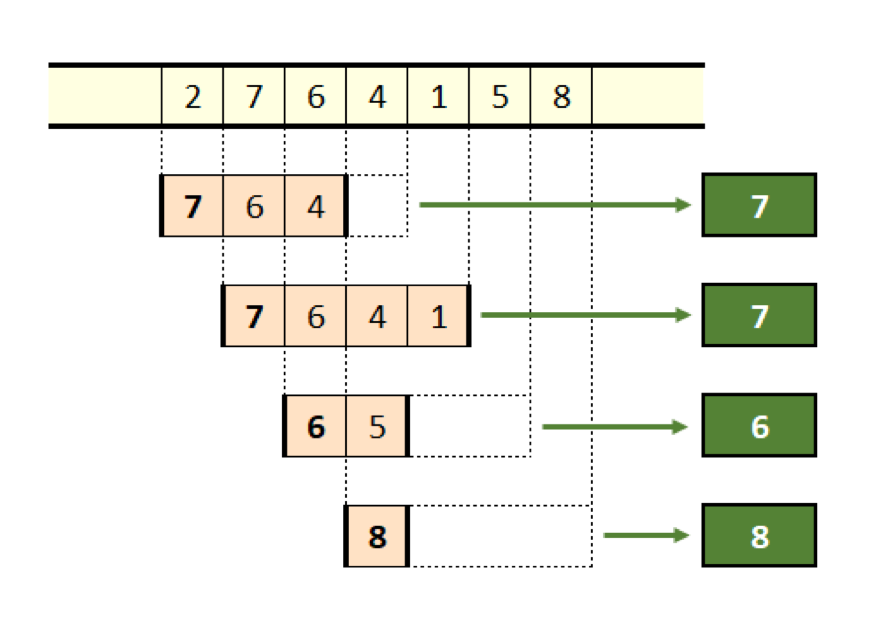
図11：各最大値

アルゴリズムの説明が終わりましたので、実装に入りましょう。普通は両端キュー（deque）をベースにして実装します。dequeとは、両端でエンキューもデキューも行えるキューのことで、本アルゴリズムの実装ではその動作を使います。

void insert_maximum_candidate(int value, bounded_deque &maximums)
{
while (!maximums.empty() && maximums.back() < value)
maximums.pop_back();
maximums.push_back(value);
}
void remove_maximum_candidate(int value, bounded_deque &maximums)
{
if (!maximums.empty() && maximums.front() == value)
maximums.pop_front();
}
int* range_maximums(int* data, int n, int k)
{
assert(data != NULL);
assert(n > 0);
assert(0 < k && k <= n);
bounded_deque maximums(k);
for (int i = 0; i < k — 1; i++)
insert_maximum_candidate(data[i], maximums);
int* result = new int[n — k + 1];
for (int i = k — 1; i < n; i++)
{
insert_maximum_candidate(data[i], maximums);
result[i — k + 1] = maximums.front();
remove_maximum_candidate(data[i — k + 1], maximums);
}
return result;
}

この解法では、fixed_dequeと名づけた独自のdeque実装を使っています。std::dequeとは異なり、このクラスではデータのバッファサイズが固定されていますが、その方が少なくとも10倍高速です。内部的には、リングバッファという極めて効率的な仕組みを取っています。fixed_dequeの実装は本記事に記載したバンドルからダウンロード可能です。ともかく、fixed_dequeクラスはstd::dequeと全く同じパブリックインターフェースを採用していますので（唯一の違いはコンストラクタがバッファサイズを予想すること）、必要に応じてstd::dequeに置き換えてください。実行速度がかなり落ちること以外、影響はありません。

前の2例と同様、この実装の時間計算量を求めてみましょう。シーケンスから入力された値はどれも、必ず1度だけエンキューされ、多くて1度デキューされます。したがって、入力数値1個につき多くて2つの動作が発生するので、アルゴリズム全体の時間計算量はO(n)です。また、このアルゴリズムでは、ウィンドウサイズkに対して空間計算量O(k)が追加で必要となります（前の2例のアルゴリズムで必要なのは空間計算量O(1)のみ）。

次の面接に向けて準備中で、もっとうまく、もっと速く解答できるようになりたいという方は、コーディング問題をPrampで受験仲間と生練習してみるといいでしょう。

型にはまらずに考える

以上、スライディングウィンドウに基づいた3種類のアルゴリズムを見てきました。そのいずれも、実行時間はお約束したとおりO(n)でした。本記事を終える前に、このスライディングウィンドウの手法が2つの大きく異なる分野でどのように応用されているかをご紹介したいと思います。

1つは、TCP/IPのようなパケットルーティングプロトコルの分野です。スライディングウィンドウは、インターネットプロトコル（IP）の信頼性を上位の伝送制御プロトコル（TCP）で高めるために採用されています。IPはパケットが送信された時と同じ順序で受信されることを保証しませんが、TCPがまさにそれを保証するわけです。つまり、スライディングウィンドウはTCP/IPプロトコルスイートが成功できた一握りの決定的要因の1つとなっているのです。

TCP受信者はパケットを受信するためのウィンドウを保持します。パケットが信頼性の劣る（ただし実用性はより高い）IP経由で到着すると、送信時とは違った順序でウィンドウ内の個々の位置に到着するかもしれません。しかし、一番左のパケットが到着次第、TCPウィンドウは最大限右にずれ、全ての連続したパケットについて送信者に確認応答を送り、それらのパケットを出力します。すると、それを合図に送信者は次のパケットをIPネットワークへ送り始めるのです。

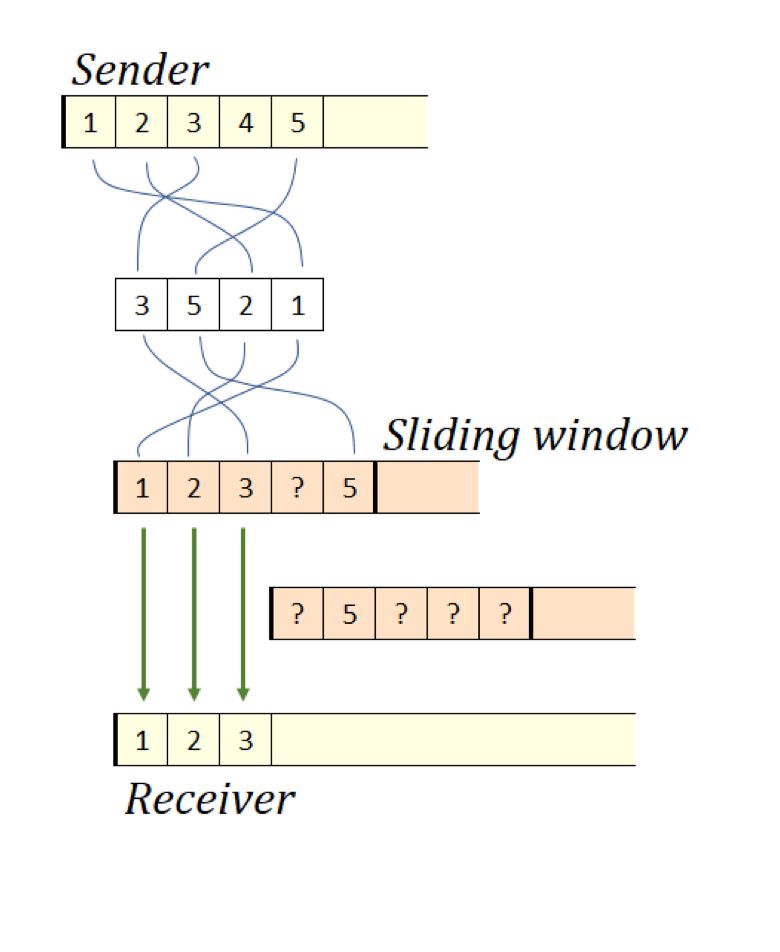
図12：TCP/IP

もう1つの応用分野（であり本記事最後のセクション）が何であるかは、もうお分かりでしょう。

Snakeです。このゲームは何十年も前に登場したものの、多くの人に知られるようになったのはNokiaの携帯電話に搭載されてからです。

図13：Snake

どんな形で採用されたと思いますか？　ヘビ自体がスライディングウィンドウなのです！
ヘビが移動する際に描画する必要があるのは、画面全体で2個のブロックだけです。尻尾を背景の1ブロックに変え、ヘビの前にある今まで背景だった1ブロックを新しい頭にするわけですから。

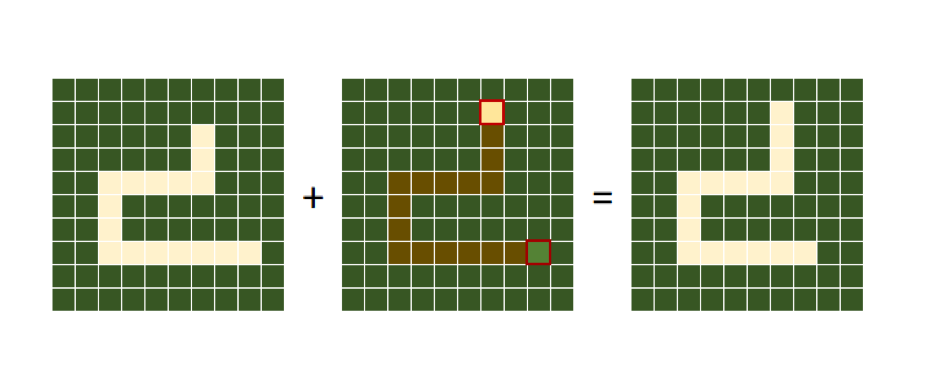
図14：Snake＝スライディングウィンドウ

スライディングウィンドウを応用した結果、このSnakeゲームでは、ヘビの長さにかかわらず1tickにつき多くて2個の原始的ブロックを描画するコストしかかかりません。そのため、Snakeは原始的ハードウェア上に実装されながらも携帯電話のバッテリーを使い果たさなかったのです。

まとめ

本記事ではスライディングウィンドウと呼ばれる一般的な手法を詳しく見てきました。このスライディングウィンドウがデータシーケンス処理アルゴリズムの最適化に応用できることを、お分かりいただけたと思います。うまくいけば、スライディングウィンドウを使ったアルゴリズムは、n個のオブジェクトを持つシーケンスに対してO(n)時間で実行できます。これは通常、アルゴリズム設計の観点から見た最も速い実行時間です。

問題解決の具体例として、今回は数値のシーケンスを扱う3種類のアルゴリズムを開発しました。3つともそれぞれ主にデータ処理や画像処理といった実世界の分野に応用可能です。だからこそ、スライディングウィンドウはアルゴリズム設計の貴重なツールとして今日まで使われ続けており、コーディング面接で取り上げられることも多いのです。

著者：Zoran Horvat
Coding Helmet Consultancyの主席コンサルタント。講演や記事執筆を100本以上手掛け、フリーのトレーナーとしても活動。