image by Schnelliboy
『ベクトルが分からない!』人にはじめから教える数学Bベクトル入門。第1回はコチラからご覧下さい。
シリーズ第2回は「ベクトルの一次独立」です。
このあたりから本格的に分からない!と言う人が出て来るので、さらに丁寧に解説して行きます。
(零(ゼロ)ベクトルや線分の種類などが曖昧な人は、入門第1回を先に読んで貰った方が理解しやすいです。)
そもそも一次独立ってなんなんだ!?言葉の意味も分からん、、、
前回は世の中には色々な「線」があって、ベクトルはその中の「有向線分」(向きがある線分)なんだよと言う話をしました。
線分:「線」の中で、両端が決まっているものの事。
今、ベクトルが一つだけあるとします。これを、仮にaベクトルとします。
x軸とy軸で表される座標上で、
始点(矢印で無い方のベクトルの端)を原点Oに置いて、向き(傾き)と大きさ(長さ)を決めると、矢印の先(終点)は一つの座標に決まります。
このはじめのaベクトルを、あえて「2つのベクトルを使って表しましょう」と言う考え方が一次独立の出発点です。
ここで何でわざわざ2つにベクトルを増やすんだ!一つでもややこしいのに(怒)と言う人もいるでしょう。
しかし数学に無駄な事は有りません。意味があるから面倒くさいと思われる事をしているのです。
その意味は、この記事の後半(ベクトルの一次独立の応用)の所で扱います。
”ベクトルの一次独立”〜言葉のイミ〜
先程2つのベクトルで一つのベクトルを表すと言いました。
この2つのベクトルをbベクトルとcベクトルと置きます(文字はなんでもokです)
そしてaベクトルを表すのでした。
ここで一次独立の意味を書きます。
一次独立とは、bベクトルが0ベクトルで無く,cベクトルも0ベクトルで無い
(=つまりbベクトルとcベクトルは長さがあると言う意味です)時に、bベクトルとcベクトルが並行でない事を言います。
*(このカッコ内の内容は理解できなくて構いません。本来、一次独立は英語では線型独立と言い、その言葉が示す様に線型代数学の領域です。そして、ベクトル空間に於いてn個の相異なるベクトル<スカラー量で表される係数部分が全て0で無い>を線型結合した時、それが0である時、線型従属と言い、逆にn個の相異なるベクトルの係数部分が全て0の時、それらを線型結合したものが0になる時、線型独立と定義されます)カッコ終わり。
そして、
ベクトルの一次独立で最も重要な事は、どんなベクトル(ココではaベクトルとします)であっても、
一次独立な2つのベクトル(bベクトルとcベクトル)で表すことができると言う点です!!(但し、平面の場合です)
これだけだと??な人もいると思うので、<図1>を見て下さい。
もう一つ大切な事は、一つのベクトル(ココではaベクトルとしましょう)を一次独立な二つのベクトル(ココではbベクトルとcベクトル)で表す時、
その係数は一通りしか無いと言う事です。これも分かりづらいと思うので<図3を見てください>。
<図1>
上の図1、2の様に、一次独立なベクトルが二つあれば、平面上のどんなベクトルも表せます!(繰り返し)
またbベクトルとcベクトルに各々sとtと言う係数が付いています。(右下)この数字を変化させる事で、
左上図1のaベクトルを左下図2の様に2bベクトル+(7/3)cベクトルで表しています。
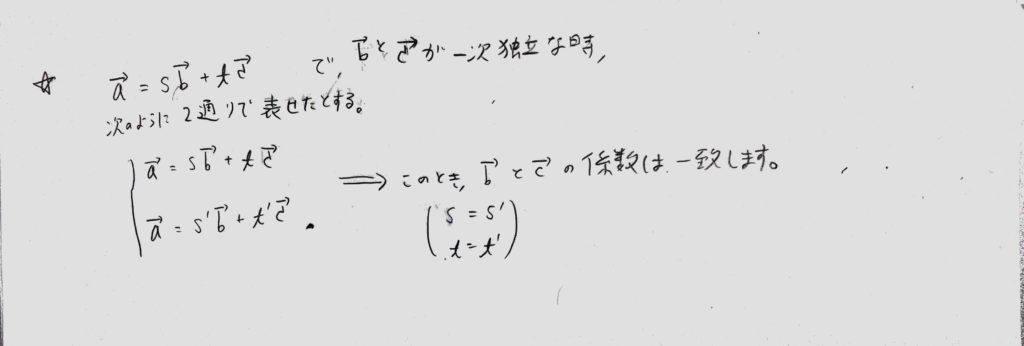
<図3>
ベクトルの一次独立の応用
ではベクトルの一次独立はどう言う風に役に立つのでしょうか?実際に例題を使って説明して行きます。
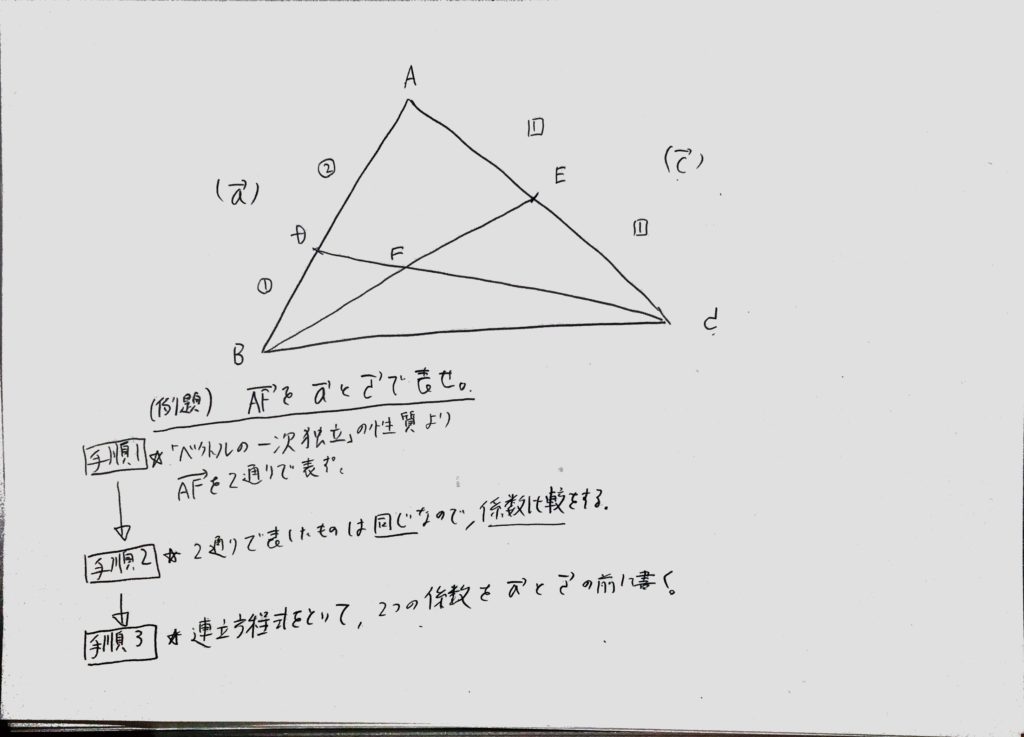
(例題)三角形ABCの辺ABを2:1に内分した点をD、辺ACを1:1に内分した点をEとして、
BE、CDの交点をFとする。この時ベクトルAFをベクトルAB(=ベクトルaとする)とベクトルAC(=ベクトルcとする)で表せ。
・・・例題の文章で嫌になっている人も居ると思うので下の図4で解答、解説を行います。
<図4>
順を追って説明します。この問題は、よく「交点の位置ベクトル」と言う範囲で頻出のタイプです。
初めて解く人にはややこしいですが、慣れるとただの計算問題になります。
手順1:とりあえず、問題はベクトルAFを書け。となっていますが、一次独立のテーマは2つのベクトルで1つのベクトルを表す事でした。
したがって、ベクトルAB(aベクトル)とベクトルAC(cベクトル)の二つで表す方法を考えて見ましょう。
ここで知っておくべき公式を紹介しておきます。
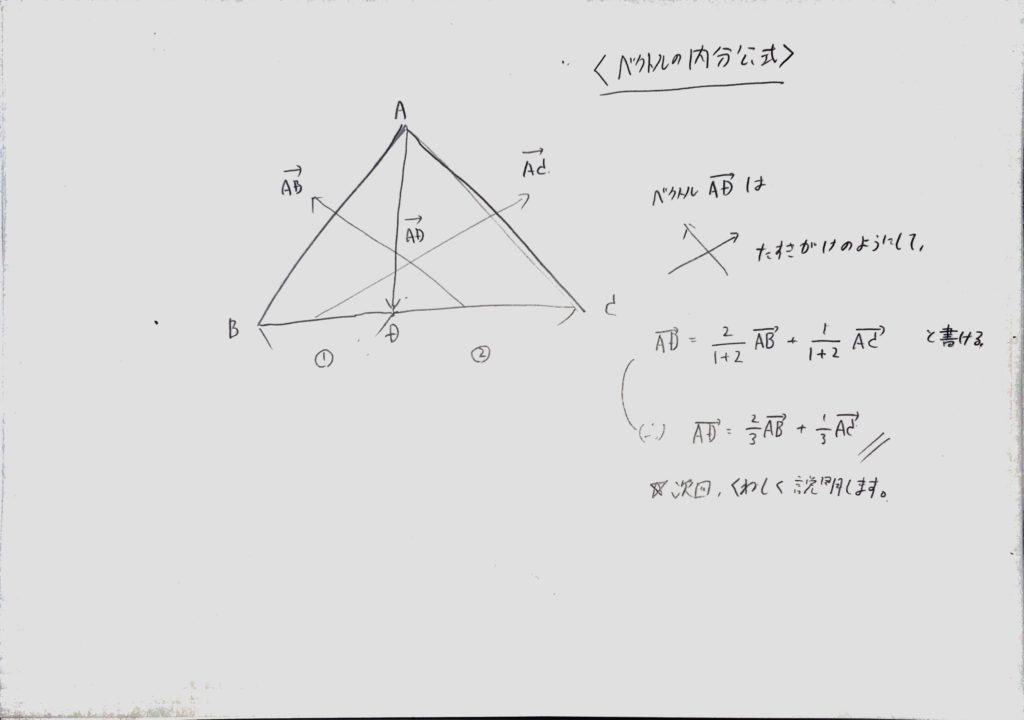
ベクトルの内分公式
三角形ABCがあった時、BCを1:2に内分した点をDとする。
この時、ベクトルAD=(2/3)AB+(1/3)ACと表すことができます。
<図5>を見てください。この様に内分した点の左右での比(ここでは1:2)をクロス(たすきがけの要領です)
して足したものとして、内分点を表すことができます。
<図5>
では手順1に戻ります。
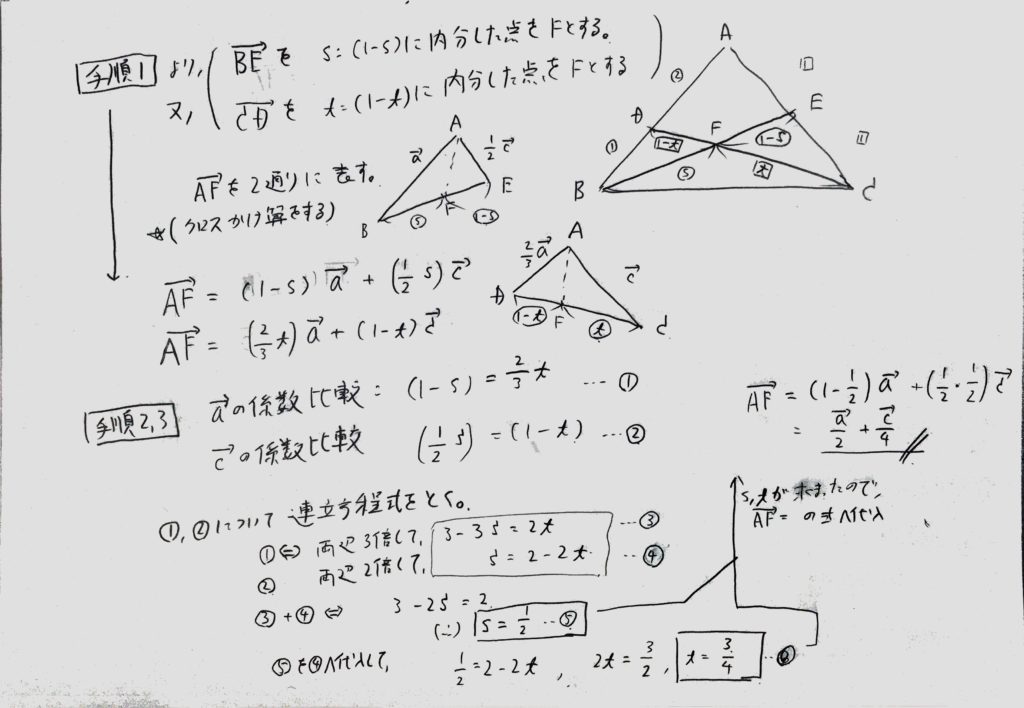
ベクトルの内分公式より、BF:FEとDF:FCが分かれば、クロスしてベクトルAFを2つ求める事が出来ます。
が、二つの比が分かりません!こう言う時は、なんでもいいので適当な文字で勝手に比を置いてしまって良いです。
但し、例題の解説にもある様にS:(1ーS)の様に比を置く訳ですが、必ず比を足したら1になる様に設定して下さい。
<図4>でもS:(1−S)とt:(1ーt)と置いていますが、どちらも足して1になりますね?
これは、証明も含めて次回:ベクトル入門第3回(内分点の位置ベクトルとそのコツ)で詳しく説明するので、
今は手順の一つとして覚えておいてください。
手順2
ベクトルAFが、内分公式より2通りに表せました。この2つのベクトルはどちらもAを始点としてFを終点とするものなので、
当然同じものになるはずです。と言う事は、ベクトルaとベクトルcの係数は同じにならないとおかしいですよね?
そこで、係数比較をすると、<図4>の丸1・丸2の様に2つの連立方程式ができます。
これを解いていくと、sとtが求まります。
手順3
後はsでもtでもどちらでもいいので、求まったs/tをベクトルaとベクトルbの係数に代入します。
これで、ベクトルAFをベクトルaとベクトルcで表せました。
・・・大分長文になりましたが、理解できましたか?
この種類の問題は本当によく出題される上、高校分野でのベクトルの中で最重要な公式や解法が詰まっているので
避けて通れないところなのです。分かりにくいところは何回も読んでみて下さい、そして理解出来たと思ったら
どの教科書や問題集でも類題があるので解いて下さい。
分からない所があれば、コメント欄に質問を書いて貰えれば出来る限り解説します。
お役に立ちましたら、はてブ!・イイね!・フォロー等でシェアしてもらえると嬉しいです!(この文の下にSNSシェアボタンがあります。)
お疲れ様でした。




