はじめに

「クラウドを支えるこれからの暗号技術」のデジタル署名の説明へのツッコミtweetをしたところ、著者の方との遣り取りが始まったのですが…。
※togetterまとめ「電子署名=『秘密鍵で暗号化』」という良くある誤解の話に経緯があります
認識の齟齬についてtwitterでどうこうするのは難しいですし、批判ばかりなのも建設的ではないので、「自分ならこう書くだろう」という文面の形でまとめてみました。

署名の説明案

前提

「クラウドを支えるこれからの暗号技術」Web公開されているPDF、2018/3/11時点(最終更新2017/11/11の4.6節デジタル署名(p.50)を、書き換えるとしたら、という前提で文面を作っています。
※そのため既存の文面の流用や、他の節を参照する記述があります。

説明案

デジタル署名とは、あるメッセージがその作者によって作られたことを検証する仕組みです。電子署名や単に署名ということも多いようです。他人がその作者になりすまして署名を作ったり、別のメッセージに対する偽の署名を作ったりできないようになっています。そのため署名したことを後で否認することができません。またそのメッセージが改竄されていないことも確認できます。

初期のアイデアは公開鍵暗号の仕組みを逆に使えないかというものでした。これは、DiffieとHellmanが1977年に公開鍵暗号と共に提唱したものです。
次のように公開鍵暗号があったとして、

つまり、メッセージを秘密鍵でsに復号し、公開鍵によって暗号化してmに戻すこと、これがもし仮に可能であるとすれば、sは秘密鍵の所有者しか作成できないデータとなりますし、一般の人は公開鍵を用いて元に戻せるかどうかを見ることで、秘密鍵の所有者が作成したことを検証できるということです。

3.16節のRSA暗号のEnc,Decを良く見ると、メッセージm、暗号文c、どちらもmod nでの剰余になっています。そのため、暗号化していないmを復号処理Decにかけることが可能です。加えて、 Dec(Enc(m))=med≡m mod n$Dec(Enc(m))=m^{ed}\equiv mmodn$ が成立したのと同じ理屈で Enc(Dec(m))=med≡m mod n$Enc(Dec(m))=m^{ed}\equiv mmodn$ が成立します。
つまり、RSAはDiffieとHellmanが提唱したデジタル署名のアイデアを実現したものとなっています。

では、デジタル署名は公開鍵暗号を元にした技術かと言うと、それは適切ではありません。その理由は大きく2つあり、ひとつは公開鍵暗号の中でもEnc,Decを逆に適用できるという特殊な条件を必要とすること、もうひとつは、今日主流のデジタル署名でRSA以外はもはや公開鍵暗号を元にした方式ではないことです。

例えば前者の例として3.11節のElgamal暗号を見ると、メッセージmに対して暗号文は(c1,c2)$(c_1,c_2)$と言う形であり、暗号化していないmを復号処理にかけることはできません。
紛らわしい話として、Elgamal暗号と同時に発表されたElgamal署名という方式があるのですが、これもElgamal暗号を逆に適用しているわけではないのです。
※ただし、Elgamal署名とElgamal暗号が共通の原理を用いている兄弟のような技術であることは確かであり、丁度「人はサルから進化した」が誤りでも「人とサルは共通の祖先から進化した」が正しいのと似た状況と言えるでしょう。

後者の例として、まだElgamal署名はElgamal暗号に似ているとは言えるものの、その応用であるDSA、楕円曲線版のECDSA、最近ビットコインで脚光を浴びるようになったシュノア署名、シュノア署名を応用した楕円曲線暗号であるEdDSA、いずれも対になるような公開鍵暗号が存在しません。
元は公開鍵暗号の逆として生まれたデジタル署名という概念ですが、その本質はあくまで(秘密鍵を持つ)本人のみが署名を作れること、(秘密鍵と対になる公開鍵を使って誰でも)署名データの妥当性を検証する手段があることと言えます。

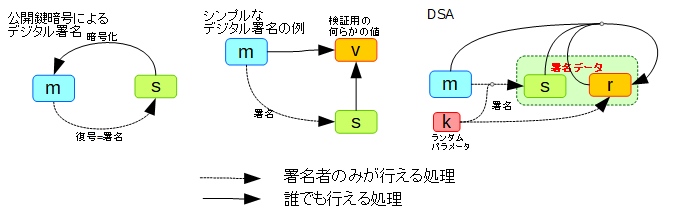
ここで、「いやいや、それを実現するために公開鍵暗号が必要なんだろう?」と思われるかも知れません。世間一般的に広くそのような(非専門家の)解説が流布されているからです。しかし次の図を見れば分かる通り、必ずしも復号を署名にあてずとも、例えばメッセージと署名データ双方から何らかの検証用の同一の値が導かれるようであれば、それで電子署名たる要件を(安全性等の議論は別にして)満たしていることになります。4.6.2節で紹介しているDSAの場合、署名データの一部である r が検証用のデータを兼ねています。

ところで MAC はメッセージが改竄されていないかを確認するために使わるものでした。MAC は二人の間で秘密鍵を共有しなければなりません。人が増えるとそれぞれの組の間で共有すべき秘密鍵が増え、管理する鍵の個数が膨大になってしまいます。デジタル署名は秘密鍵を共有することなく公開鍵のみで誰でも署名を検証できます。MAC とデジタル署名の関係は、共通鍵暗号と公開鍵暗号の関係に似ています。

元の文面での間違い

ここでは、元の文面で間違いである点を改めて指摘していきます。

• 基本アイデアは公開鍵暗号の原理を使う点にあります
  上の説明案にある通り、公開鍵暗号を元にした署名は一部でしかありません。応用が直接の延長上にないものを「基本アイデア」と呼ぶのは不適切です。歴史的な経緯を踏まえ「初期のアイデア」の方が適切だと言えます。
• 秘密鍵Kで暗号化して公開鍵K'で復号できます
  これは一般にも良く見られる典型的なネタなのですが、RSAに限っても正しくは「秘密鍵で復号」「公開鍵で暗号化」です。DiffieとHellmanの提唱したデジタル署名でも、RSAの最初の論文でも「秘密鍵で暗号化」とは書いていません。
• 公開鍵暗号はそのままデジタル署名として使えるわけではありません
  「デジタル署名として使えるわけではない」そのこと自体は間違いではありませんが、この書き方であれば「工夫すれば使えるのね」という誤解を与えかねません。おそらくElgamalあたりがなんとなく説明できるようにという意図もあるのでしょうが、「公開鍵暗号がデジタル署名に使えるためには特殊な条件を必要とする」位が適切です。
• 一般に公開鍵暗号の公開鍵と秘密鍵の形は違うので両者を入れ替えることはできないからです
  「秘密鍵で暗号化」という間違った説明に合わせようとしているため、この説明自体意味をなしていません。鍵の違いは問題の核心でもなんでもなく、暗号化していないメッセージを直接復号できるか、そして暗号化によって元に戻せるかがポイントだからです。
  ※ついでに言えば今RSAで使われる公開鍵・秘密鍵、データを見比べてみれば違う形をしているのが分かります。そのためRSAが署名に使えることと論理矛盾を起こす説明になってしまっています。
• XX暗号の考え方を用いてXX署名が作られています
  • Elgamalについては似ているので微妙なところではありますが、Elgamal暗号とElgamal署名は共通の原理に基づくくらいでしょうか。( 説明案の中のサルと進化の喩えをご覧ください )
  • Cramer-Shoupについて、元の説明が意図している暗号と署名がはっきりと分かっていないのですが、一般にCramer-Shoup暗号/署名と呼ばれるものについて、暗号の論文を見ると離散対数問題に基づく方式、署名に関連した論文を見るとRSA問題に基づく方式と、全く別物に見えます。なので恐らく間違いと言って良いでしょう。

補足

なぜ誤解の指摘を行うのかその意図

「XXが誤りである」このような指摘に関しては、必ずと言って良いほど「重箱の隅をつついているだけではないか」「定義(言葉遣い)の問題に過ぎない」と言って、故意かどうかはともかく、その指摘の意義を毀損しようという声が上がります。

もちろん、それは内容によって適切な場合があるので一概には言えないのですが、少なくとも私個人としては、重箱の隅をつつく趣味はない ( というよりそんな細かいところを気にできるほど専門家でもない ) のであって、むしろ理解の根幹に関わる重大なバグと捉えているからこそとまず断っておきます。

誰にとって有用か

誤解を恐れずはっきりと言ってしまえば、キーワードだけ拾えればそれで良い人にとっては、この記事の内容はどうでも良いことです。むしろ間違いであろうとなんだろうと、はっきりとイメージしやすいモデルを提供してくれる方が有用でしょう。
※例えばCramer-shoupの暗号と署名が本当は別物だからと言って、使う機会がある人もそういないでしょうし、困る話ではないのです。というか、私も初めて知りました。

ただし、(人によっては難易度の高い)数学の話も消化し、様々な方式の実体に迫りたい、そう望んでいる人には、今回取り上げた誤解というのは目に見えない重い足かせとなる恐れがあります。むしろ細かい所はどうでも良くて、本質を外していること、それが仇となって内部に矛盾を孕んだ説明になること、これはなかなか厄介です。
「秘密鍵で暗号化、だけど暗号としての意味はない…なにそれ?」「公開鍵暗号の考えから署名が作られる、でもDSAに暗号化の機能はない。??」答えは簡単で、(狭義の)公開鍵暗号とデジタル署名は別物だから。
「公開鍵で元のメッセージに戻せれば正しい署名、と。…DSAってどうやって戻してるの?」別に戻すのが署名の本質ではなくて、何らか検証手段があることが本質、その手段は様々ということです。

人というのは思った以上に言葉によるイメージに引きずられます。一旦「署名=暗号化」というイメージができあがると、それに沿わないものを受け入れるのに大きな抵抗が生まれます。何かが同じだという説明を見ると、実際に存在する違いに気付けなくなります。だからこそ「技術書」として説明を著す方には、深い理解と慎重な言葉使いが求められるところだと思います。ただ「技術書」でないのであれば、それを期待するのも酷なところはあるかもしれません。

長くなりました。様々な署名方式の理解を深めたいという方には、流通している説明を一度は疑ってみてほしいと思います。今回の指摘がそのきっかけになれば幸いです。

RSAに関する誤解

「いやいやそうは言っても、RSAでは暗号化と復号は同じだし、公開鍵と秘密鍵は取り換えられるじゃないか。間違いとまでは言えないだろう?」そういう声もありそうなのですが、実はRSAに関しても誤解があると言えます。ここではそれについても触れておきたいと思います。

秘密鍵で暗号化?

これについては説明案でも触れましたが、そもそも「秘密鍵で暗号化」なんてDiffieとHellmanも、RSAも言ってないんですね。「秘密鍵で復号」です。後発の論文なり専門の技術文書でもそうです。良く分かってないなら専門家の言を逆に変えてしまうの止めましょうよ、というのがまず1つ。
※ついでに言うと、大学の専門のテキストなりで署名の説明を見ても、今日では「秘密鍵で暗号化」はおろか「秘密鍵で復号」なんて文言は出てきません。専門家の言葉を尊重するなら、やはり署名を公開鍵暗号ベースで説明するのは不適切なのです。

暗号化と復号は同じ?

いやしかし、RSAの暗号化 c=me mod n$c=m^{e}modn$ と復号 m=cd mod n$m=c^{d}modn$ 同じじゃないか。m,cとe,dが違うだけ。逆にして何の問題があるのか、と思われるかも知れません。
確かに式の形としては同じなんですが、そこには見落としがあります。それは値の取り扱いと各処理を行う者の立場の違いです。

公開鍵の e は文字通り公開を前提とした値です。ということは例えば特定の値に固定するような運用の余地も考えられます。実際、現行のRSAでは e の値は 65537 と固定で使われることが多いようです。公開鍵を使う暗号化/署名検証処理も、これに沿って最適化を施すことも考えられるわけです。
一方で秘密鍵の d は固定なんてできませんし、総当たりで破られても困りますから、e に比べて遥かに大きな値になるのが普通です。
この違いは、実際に暗号化/署名検証、復号/署名作成の速度にも現れます。2つの処理が同じだと考えていると処理速度も同じなのではないかと思うかもしれませんが ( 気の利いた人ならむしろ逆の結果と勘違いすることも )、実際問題 e,d の違いから復号/署名作成の方が圧倒的に遅いのです。

もう一つは mod n の計算です。ここにどんな違いがあるのか? と思われるかも知れませんが、RSAが素因数分解の困難さを利用した方式であったことを思い出してください。つまり、暗号化/署名検証側は n の素因数分解の結果を知らない一方で、復号/署名作成側は、n=pq の結果を知っているという立場の違いがあるのです。
オリジナルのRSAではこの違いを活かした何かはまだ生まれていませんでしたが、おそらく2001年に発表された中華風剰余定理による最適化が、各処理系に採用され、今でも使われています。

例えばメジャーな暗号化ツール/ライブラリであるOpenSSLの場合、次のコマンドで適当に公開鍵・秘密鍵の組を作って内容を見てみると、構成がずいぶん違うことが分かります。

$ openssl genrsa 32 2>/dev/null | tee >(openssl rsa -pubout 2>/dev/null | openssl rsa -pubin -text -noout >&2) | ( sleep 5; echo; openssl rsa -text -noout >&2)
Public-Key: (32 bit)
Modulus: 2657941441 (0x9e6cf7c1)
Exponent: 65537 (0x10001)

Private-Key: (32 bit)
modulus: 2657941441 (0x9e6cf7c1)
publicExponent: 65537 (0x10001)
privateExponent: 1458268601 (0x56eb69b9)
prime1: 53003 (0xcf0b)
prime2: 50147 (0xc3e3)
exponent1: 24575 (0x5fff)
exponent2: 22921 (0x5989)
coefficient: 7776 (0x1e60)

※modulus が n、Exponent/publicExponentが e、privateExponentが d、prime1,prime2が n=pq における p,q、exponent1,exponent2 が d,p,q から導出される値、coefficientがp,qから導出される値です。

もちろん、これらの違いが大きいか細かいか、それは判断が分かれるところだろうとは思いますが、これらを知ってまだ「同じだから逆にしても大丈夫」と言えるとしたら、なかなか強い心臓だなあと思う所です。
※もちろん、式の形が同じだから暗号化/署名検証と復号/署名生成が似ているという判断は妥当です。

「メッセージを暗号化」の方が理解しやすい?

著者の方との遣り取りで、「『秘密鍵でメッセージを復号』では理解し辛いのではないか、『秘密鍵でメッセージを暗号化』の方が分かり易い」という趣旨の話があり、興味深かったので取り上げます。

なるほど確かに、暗号化していないメッセージをいきなり復号するというのは、目にした人が戸惑う記述かも知れません。…ですがちょっと待ってください。その特殊な条件が成り立つことこそが、RSAを署名としても使えることの本質だったはずです。

つまり、「暗号化していないメッセージを復号する」という表現の分かりにくさは、公開鍵暗号を元にした署名のややこしさを反映したものであって、それを分かり易いだろうという理由で「暗号化」に変えてしまうのは、ややこしい部分の説明を誤魔化したに過ぎないということです。

「しかしややこしい部分に踏み込むのは…」と言う話になりかねないのですが、そもそも「暗号化していないメッセージを復号する」がなぜ分かりにくいかと言うと、「公開鍵暗号を逆に適用することこそが署名」という思い込みがあったからではないでしょうか。RSAの、しかも誤った解釈に縛られている故の幻と言うことです。「RSAの逆変換がたまたま署名に使えた」という理解なら、こんな混乱は起きなかっただろうと思います。

終わりに

ということで、著者の方に「書きます」と宣言していたので仕上げました。

…実は、評価の高い、結城さんの「暗号技術入門」も、殊署名に関して言えば ( というより公開鍵暗号全般と言って良いかも ) 同じような大きな問題を抱えている訳ですが…。なかなか難しい所ですね。