強化学習の基本 Qラーニングを直観的に理解するためのアニメーションによる可視化

経路探索問題を強化学習で解き、その過程をアニメーションで可視化しました。
↑↓で速度調節、Spaceで最速の学習、ドラッグ or タップで障害物の追加ができます。
これにより、強化学習で何をしているのか直観的に分かりやすくなりました。

問題設定

本アニメーションで可視化している問題の設定は、下記の通りです。

• 条件

  • n×n$n\times n$のマスからなる離散的なフィールド
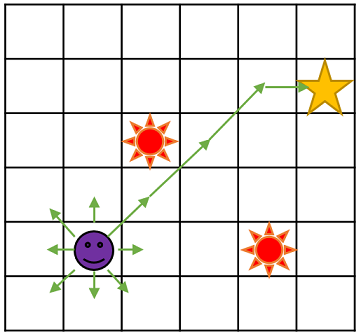
    • 固定の初期位置と目標位置(⭐)、障害物が配置されている
  • 障害物（🔴）は、踏んだら死ぬ。初期位置からやり直し
  • 自機(👾)は単位時間に8方向のいずれかへ1マス移動できる
    • 横移動と斜め移動のコストは同じ

• 得たい出力

  • 初期位置から目標位置までの、障害物を回避した最短経路

この問題を強化学習のフレームワークに落とし込み、Qラーニングで求解しています。
詳細は後述します。

各インジケータの意味

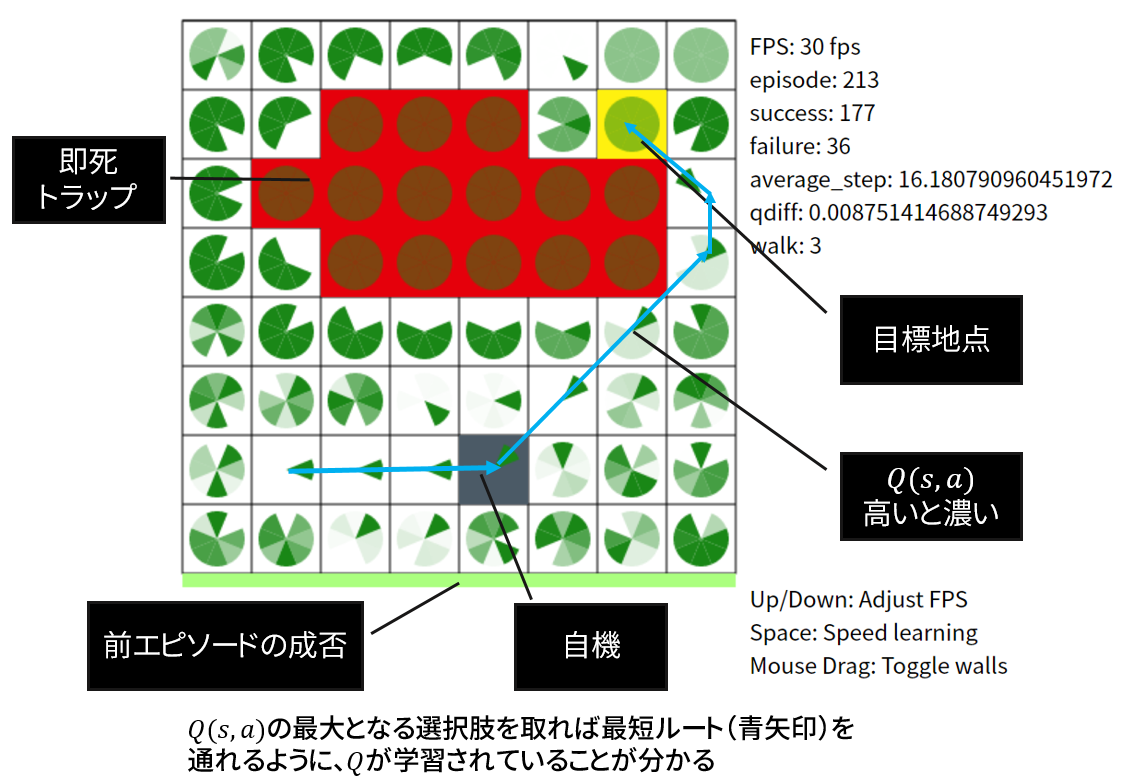
本可視化の見方を説明します。
前節で述べた問題をQラーニングで解く過程を可視化しています。

詳細

上記の可視化で表現したかった数式などを説明します。

問題を強化学習のフレームワークに落とし込む

強化学習の用語を先に説明した経路探索問題に当てはめると、下記の対応となります：

• 状態 s$s$ : 自機のいるマスの位置
• 行動 a$a$ : 上下左右斜め8方向の内、進む方向
• 方策 π(a|s)$\pi (a|s)$ : あるマス目s$s$において、どの方向a$a$へ進むか = 進むべき経路を示す
• 報酬 R(s,a)$R(s,a)$ : あるマス目s$s$において、ある方向a$a$に移動した結果の評価
  • 障害物を踏んだ → -100 の報酬を与える
  • 目標位置に到達した → +50 の報酬を与える
  • それ以外 → -1 の報酬を与える

この設定で強化学習を行うと、問題の解を得ることができます。
本可視化では、Qラーニングを用いて解いています。

数式で見る

各マスに表示されている緑パックマンのようなものは、行動価値関数Q(s,a)$Q(s,a)$の値の大きさを示します。
本問題においては、状態s$s$はマス目の位置、行動a$a$は8方向のどれかを示します。

行動価値関数Q$Q$とは、ある時刻において状態がs$s$のとき行動t$t$を取ったときに以後得られるリターンの期待値を表します（なるほどわからん）。
とにかく、Q(s,a)$Q(s,a)$が最大となるa$a$こそが、今後のリターンが一番大きいということで、s$s$における最適の行動であると言って良いでしょう。

実際、最適な行動価値関数Q∗(s,a)$Q^{\ast }(s,a)$が求まれば、最適方策π∗(a|s)${\pi }^{\ast }(a|s)$は直ちに

と求めることができます。
方策 π(a|s)$\pi (a|s)$ とは、状態s$s$のときに行動a$a$を取る確率を表すものなので、全てのs$s$についてそれぞれ行動価値関数が最大となる行動a$a$を常に（確率=1）取ることが最適な方策というわけです。

実際、本可視化におけるQ(s,a)$Q(s,a)$を見れば、進むと死ぬ方向や目標から遠ざかる方向はQ$Q$が小さく（薄く）なり、一方最短経路に従う方向はQ$Q$が大きく（濃く）評価されていることが見て取れますね。

ではどうすれば最適なQ$Q$を得られるんだという話になりますが、その一つの方法として下式に示すQラーニングを利用できます。

Qラーニングの解説記事はネットに沢山あるので、ここでは詳細を割愛することにします。
上式を実装してエピソードを重ねるうちに、Q(s,a)$Q(s,a)$は最適な値へ収束していきます。
収束した後はただ最適経路をなぞるのみということは、もう見ていただけたでしょう。

この行動価値関数Q$Q$を学習していくというイメージを持っていれば、強化学習の話題がもう少しとっつきやすくなるはずです。
一般に多くの問題ではs$s$やa$a$の空間が広大なので、今回のようなQ$Q$のテーブルに頼った手法は使えません。
代わりにQ$Q$を連続な関数として扱い、その関数を近似します。その関数近似に深層ニューラルネットワークを用いたのがDQNです。
つまり、結局原理は同じなわけですね！

まとめ

• 強化学習の一種であるQラーニングを用いて、経路探索問題を解いた
• 解く過程をアニメーションで可視化することで、仕組みが分かりやすくなった（はず！）
• ここで得られた強化学習のイメージは、古典的なQラーニングから割と最新のDQNにまで適用可能です

参考文献

• UCLの講義資料
  • ゼロから説明されていて、分かりやすいです
  • Q学習に関連する話は第2回と第6回にあります