Tree: 親子関係の付け替え
この記事はHaskell Advent Calendar 2017に投稿したものです.
関数プログラミングでは,ツリー構造はさまざまなデータの集まりを表現するのに便利なデータ構造です.
単純でよいなら,Haskell(GHC)ではcontainersパッケージにある,Data.Treeモジュールを使ってTree型で表現するのが楽です.
import Data.Tree
data Lab = A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
deriving (Eq,Ord,Enum,Bounded,Show,Read)
sample :: Tree Lab
sample = Node A [Node B [Node C [Node D []
,Node E []]
,Node F [Node G []
,Node H []]]
,Node I [Node J [Node K []
,Node L []]
,Node M [Node N []
,Node O []]]]
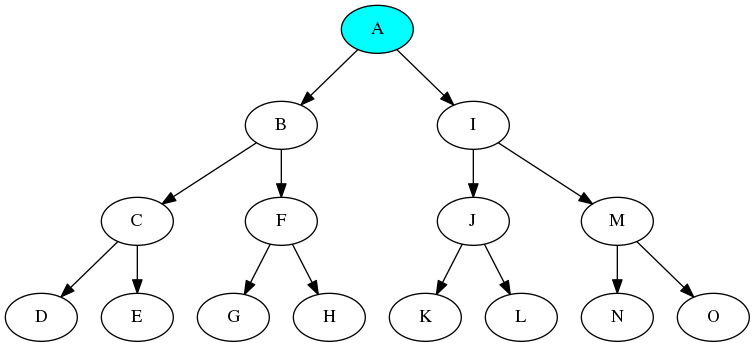
有向木
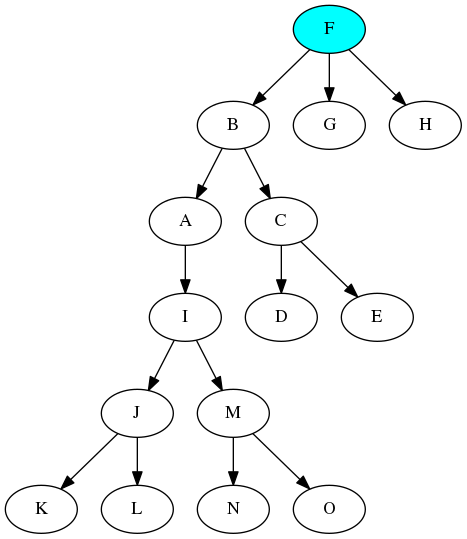
この木を描くと以下の図のようになります。
Tree a型の構造は,このように根ノードから葉ノードへ向う根付き有向木を表現したものと考えられます.このような根付き有向木は,ルートノードからはすべてのノードが到達可能です.
しかし,各ノードは自分の親ノードについては何も知らないので,任意の2ノード間のパスを調べるたりするには工夫がいります.
ここでは,その工夫を考えてみましょう.
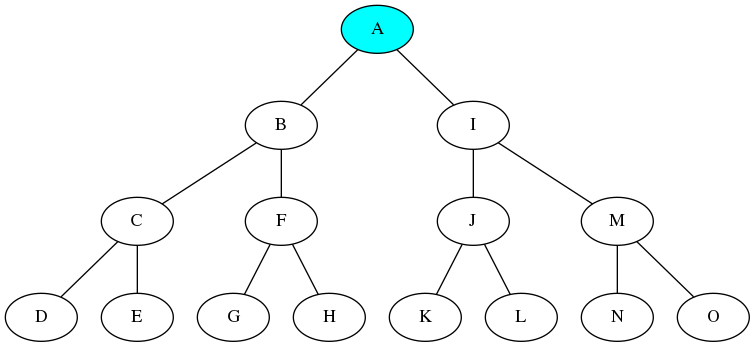
無向木
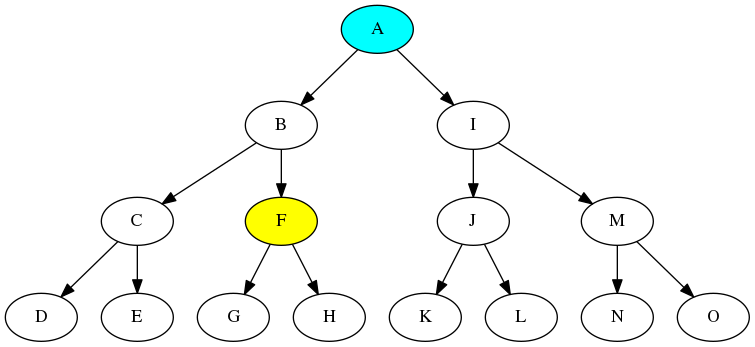
さきほどの木を描いたものを再掲します.
再掲とはいいましたが,ちょっとだけ変更してあり,無向木になっています.有向木のときにはすべてのノードへの到達経路があるのは唯一ルートノードだけでした.無向木にするとどのノードから出発しても任意のノードに到達できることがわかります.どのノードでもルートノードになれるということです.
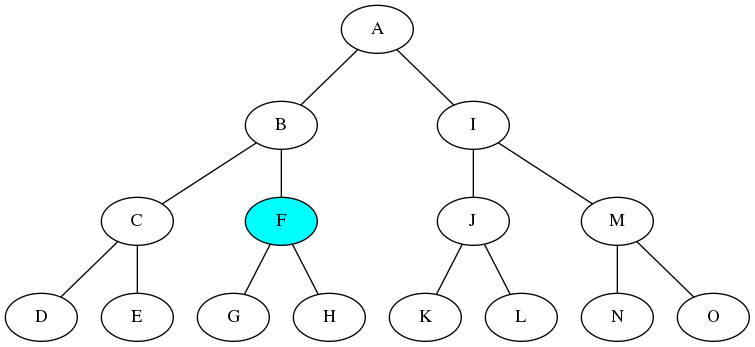
たとえば,ノードFもルートになれるのです.
ルートノードを別のノードに変更する
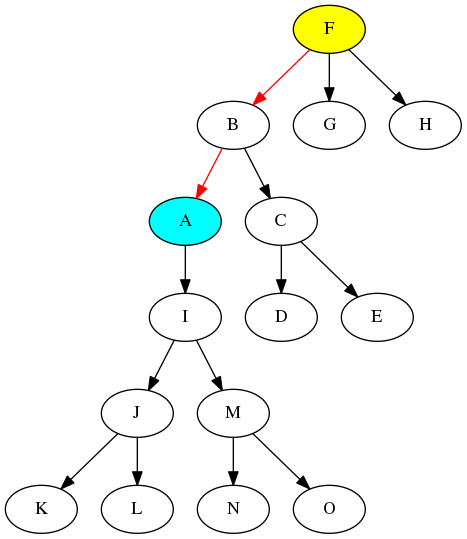
試しにFのノードを摘んで引き上げてルートノードに見立てましょう.
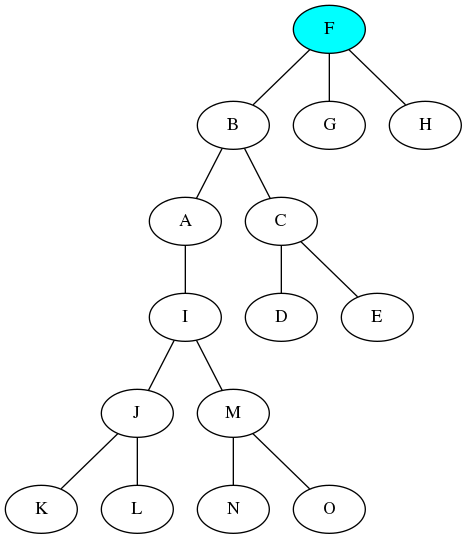
無向木であれば、Aノードをルートノードとして描いたものと、Fノードをルートノードとして描いものも、同じグラフです。これを、Fノードをルートノードとする有向木にすると
となり,さらにこれをTreeにすると、
reparented :: Tree Lab
reparented = Node F [Node B [Node A [Node I [Node J [Node K []
,Node L []]
,Node M [Node N []
,Node O []]]]
,Node C [Node D []
,Node E []]]
,Node G []
,Node H []]
となります.さて,ここから本題です.sample :: Tree Labと,ノードFを指定して,reparented :: Tree Labを生成するにはどうするかを考えましょう.
reparent :: a -> Tree a -> Tree aをどう構成するかを考えていきます.reparentの引数はどのノードをルートノードにするかの指定です.ここでは,TreeのrootLabelフィールドはノードIDとして機能するという仮定をしておきます.ノードIDで指定したノードがない場合も考えてreparentの型シグネチャは,
reparent :: Eq a => a -> Tree a -> Maybe (Tree a)
(aがノードID)としましょう.reparentの構成は,
- ノードIDで指定したノードを探して(
search) - それをルートノードに昇格させる(
promote)
でいいでしょう.
reparent x = maybe Nothing (Just . promote) . search x
ノードIDで指定した,ノードを見つけたとして,それをルートノードに昇格させる方法(promote)から考えましょう.最初の図で説明したようにTree構造は有向木になります.
ノードの昇格
それでは,たとえば,ノードFをルートノードにするにはどうすればいいでしょう.
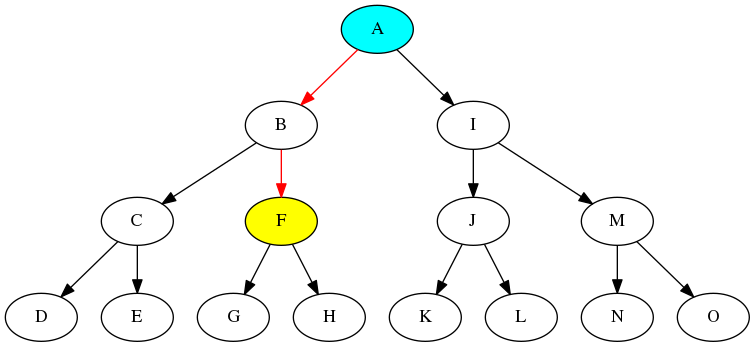
そうですね,ルートノードAからノードFまでのパスにある辺,A → B と B → F の向きを逆転して,B → A と F → B のようにすればいいですよね.
これを
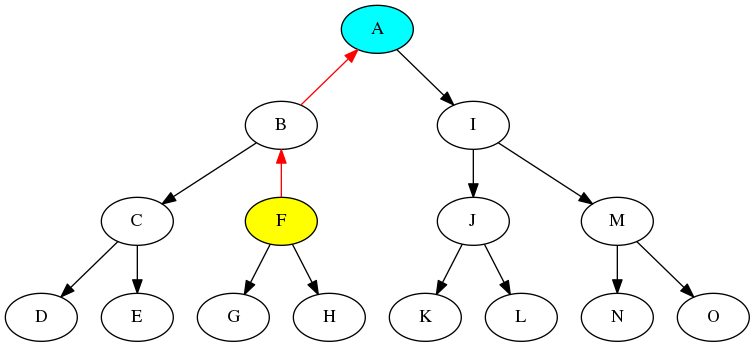
とすればよいだけです.これでノードFを最上位に描画すれば,
となって,目的の木が得られます.
簡単にいってしまいましたが,ルートノードAからノードFまでのパス情報が必要です.どうしましょう?
そうです,Arunekoさんもお勧めの(Zipperに挑む)のZipperです.
Zipper
Tree用のZipperは現在のノードとパン屑リストとの対です.
type Zipper a = (Tree a, [Crumb a])
current :: Zipper a -> Tree a
current (n,_) = n
crumbs :: Zipper a -> [Crumb a]
crumbs (_,cs) = cs
としましょう.パン屑Crumb aは以下のように定義しましょう.
type Crumb a = ([Tree a], a, [Tree a])
elders :: Crumb a -> [Tree a]
elders (es,_,_) = es
parentLabel :: Crumb a -> a
parentLabel (_,a,_) = a
youngers :: Crumb a -> [Tree a]
youngers (_,_,ys) = ys
パン屑の1つめの要素は兄姉ノードのリスト,2つめは親のルートラベル,3つめは弟妹ノードのリストです.
TreeとZipperの相互変換は以下のようにします.
toZipper :: Tree a -> Zipper a
toZipper = (,[])
fromZipper :: Zipper a -> Tree a
fromZipper = current . upMost
Zipperの上への移動upと最上位への移動upMostとを定義しましょう.
up :: Zipper a -> Maybe (Zipper a)
up z = case crumbs z of
[] -> Nothing
(b:bs) -> Just $ (Node (parent b) (elders b++current z : youngers b), bs)
upMost :: Zipper a -> Zipper a
upMost z = myabe z upMost (up z)
promoteの実装
現在のノードを含むZipperがあれば,現在ノードからルートへ,パン屑リストを使って遡れるので,promoteは以下のように実装できそうです.
promote :: Zipper a -> Tree a
promote (t,bs) = fromZipper (foldl f (t,[]) bs)
where
f (Node lab cs, ds) (ps,r,qs) = (Node r (ps ++ qs), ([],lab,cs) : ds)
searchの実装
promoteはZipperを必要としますので,search xをTree aに適用すると,ノードIDがxであるようなノードを現在のノードとして含み,パン屑リストはルートからそのノードまでのパスを示すものですようなZipperになるはずですね.
search :: Eq a => a -> Tree a -> Maybe (Zipper a)
search x t = listToMaybe (searchDown x (toZipper t))
これにはZipperを下へたどる仕組みsearchDownを利用することにしましょう.
searchDown :: Eq a => a -> Zipper a -> [Zipper a]
searchDown x z@(Node y ys, bs) =
bool id (z:) (x == y) (concatMap (searchDown x) (downs z))
downsはZipperの下への移動です.複数ありうるのでZipperのリストで表しています.
downs :: Zipper a -> [Zipper a]
downs (Node r rs, bs) = map zipper (select rs)
where
zipper (ps,x,qs) = (x,(ps,r,qs):bs)
select :: [a] -> [([a],a,[b])]
select = para f []
where
f x (xs, yss) = ([], x, xs) : map (add x) yss
add y (ys,z,zs) = (y:ys,zs)
para :: (a -> ([a], b) -> b) -> b -> [a] -> b
para _ e [] = e
para f e (x:xs) = f x (xs, para f e xs)
selectはリスト上のある種のZipperのリストですが,ここでは,paramorphismのインスタンスとして定義してあります.
というわけで、今回は『「木」配りのススメ』でした。(嗚呼GGネタ)