本日は
pythonで使えるグラフ描画ツール Bokeh の練習として行列演算の結果の可視化をしてみようと思います.
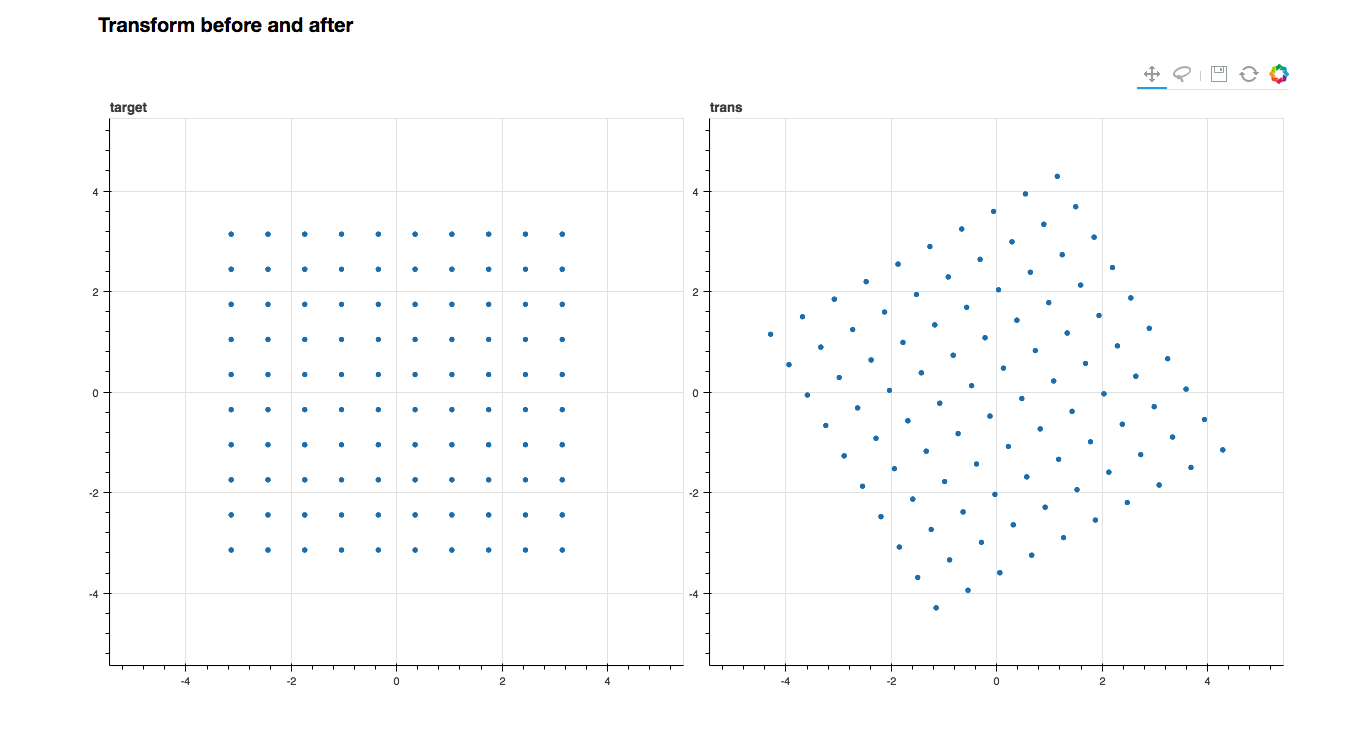
例えば, 2x2行列
は2次元ベクトルに作用させると結果が だけ回転したベクトルを出力することがよく知られています.
これを実際に Bokeh をもちいて確認してみましょう.
実装例
rot.py
import numpy as np
from bokeh.plotting import figure, output_file, show
from bokeh.models import ColumnDataSource, Div
from bokeh.layouts import gridplot, column
def main():
xs = np.linspace(-np.pi, np.pi, 10)
ys = xs
Xs, Ys = np.meshgrid(xs, ys)
Xs, Ys = Xs.flatten(), Ys.flatten()
theta = np.deg2rad(30)
mat = np.array([[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
transXs, transYs = mat @ np.array([Xs, Ys])
output_file("lasso_selector.html")
TOOLS = "pan,lasso_select,save,reset"
source = ColumnDataSource(data=dict(Xs=Xs,
Ys=Ys,
transXs=transXs,
transYs=transYs))
f = figure(tools=TOOLS, title="target",
x_range=(-np.pi*np.sqrt(2)-1, np.pi*np.sqrt(2)+1),
y_range=(-np.pi*np.sqrt(2)-1, np.pi*np.sqrt(2)+1))
f.circle('Xs', 'Ys', source=source)
transf = figure(x_range=f.x_range,
y_range=f.y_range,
tools=TOOLS,
title="trans")
transf.circle('transXs', 'transYs', source=source)
grid = gridplot([[f, transf]])
show(column(Div(text="<h2>Transform before and after</h2>"),
grid))
if __name__ == '__main__':
main()
install
$ pip install bokeh
実行例
$ python rot.py
実行すると output_file で指定した lasso_selector.html が生成され, ブラウザでこれを閲覧することができます.
ここでは格子点領域が左回りに30度回転している様子がみられます. ただ,この場合では どの点がどの点に移動した かがわかりません.
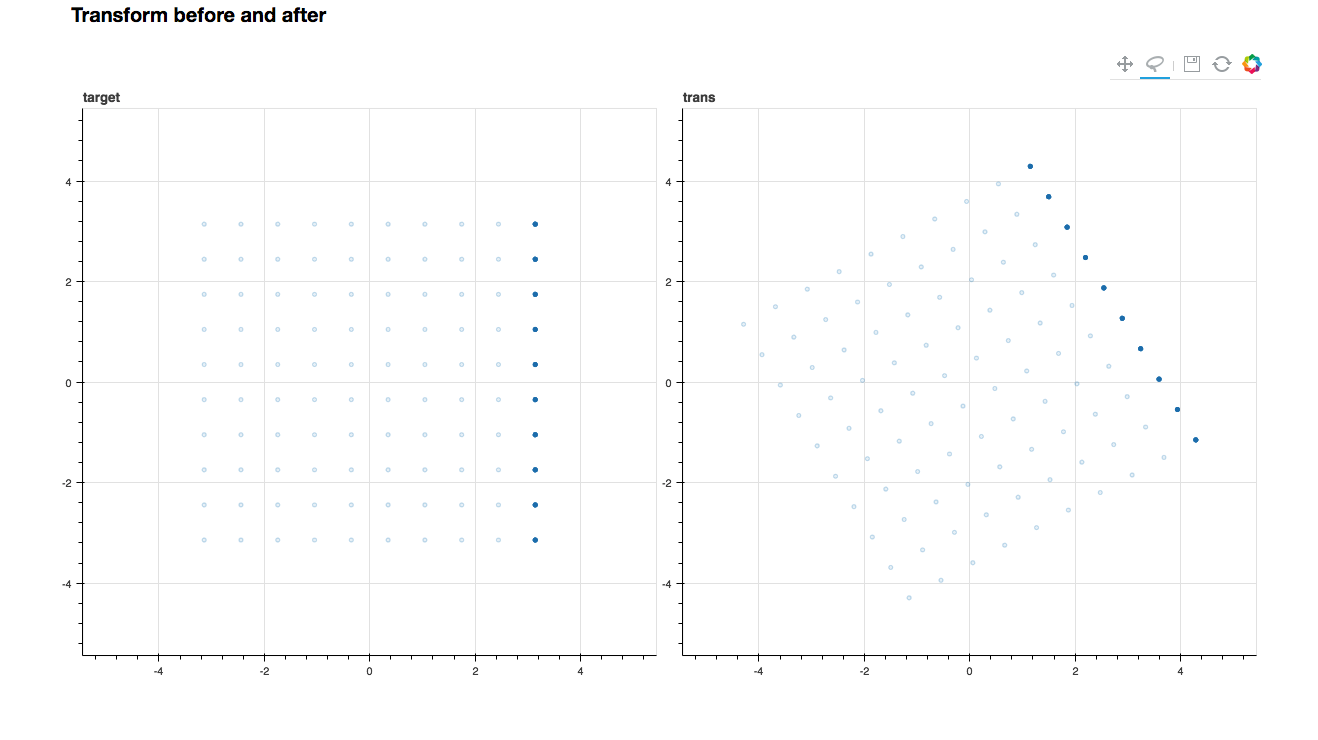
そこで, TOOLS に lasso_select を追加しすることで縄で範囲を指定した部分の targetグラフ と transグラフ の点との対応を閲覧することができます. つまり,下の図のように可視化することができます.
縦に並んだ点列が30度傾いていますね.
応用
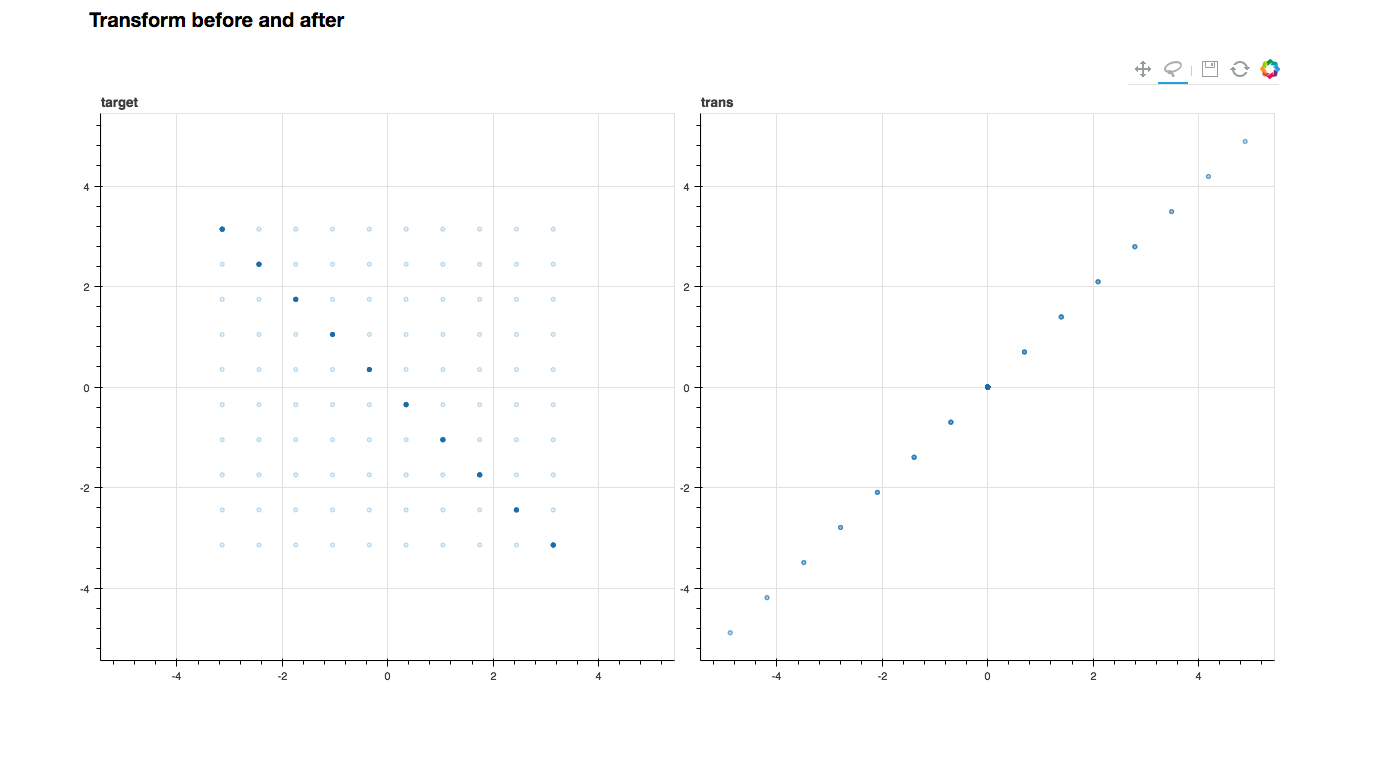
rank が1の行列たとえば,
の像をみてみましょう.
rankが1なので像は一次元平面上にズベーっと並びます. そしてtransグラフの方で原点の点を囲んでみましょう. そうすると target グラフの方では を満たす直線上の点が浮かびあがるはずです.要するに を可視化していることになります.
これから線形代数の次元定理
が成り立つのも確認できますね.