はじめに
初投稿かつn番煎じです
数独について
数独とは
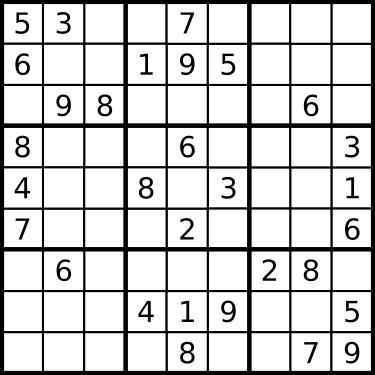
↑こういうやつ
- 3×3のブロックに区切られた 9×9の正方形の枠内に1〜9までの数字を入れるペンシルパズルの一つ
- ナンプレともいう
数独のルール
- 空いているマスに1〜9のいずれかの数字を入れる
- 縦・横の各列及び、太線で囲まれた3×3のブロック内に同じ数字が複数入ってはいけない
Z3について
Z3とは
- Microsoft Research が開発したSMTソルバ
- MITライセンス
SMTソルバとは
- 一階述語論理式の充足可能性を判定してくれる
- 充足可能(SAT)の場合は充足割り当て解の一つを出力してくれる
- 充足不可(UNSAT)の場合は出してくれない(そりゃそうだ)
解いてみる
準備
- githubからz3を拾ってくる
今回解く問題
数独問題集上級001を解いてみます
実装
- Python3で実装しました
# -*- coding: utf-8 -*-
# z3をインポート
from z3 import *
#全ての変数valは1<=val<=9であることの制約を追加するメソッド
def betweenOneToNine(val,s):
for i in range(n):
for j in range(n):
s.add(1 <= val[i][j], val[i][j] <= n)
#rowがそれぞれ他と値が異なっていることの制約を追加するメソッド
def distinctRow(val,s):
for i in range(n):
tmpList = []
for j in range(n):
tmpList.append(val[i][j])
s.add(Distinct(tmpList))
#columnがそれぞれ他と値が異なっていることの制約を追加するメソッド
def distinctColumn(val,s):
for i in range(n):
tmpList = []
for j in range(n):
tmpList.append(val[j][i])
s.add(Distinct(tmpList))
#ブロックの中身がそれぞれ他と値がことなっていることの制約を追加するメソッド
def distinctBlock(val,s):
for k in range(3):
for l in range(3):
tmpList = []
for i in range(3):
for j in range(3):
tmpList.append(val[3*k+i][3*l+j])
s.add(Distinct(tmpList))
#あるマス目に任意の数値をセットすることの制約を追加するメソッド
def setNum(val,s,x,y,num):
s.add(val[x-1][y-1]==num)
#数独問題集上級001の問題設定の制約を追加するメソッド
#http://www.sudokugame.org/archive/printsudoku.php?nd=2&xh=1
def setProb001(val,s):
setNum(val,s,2,6,1)
setNum(val,s,2,8,8)
setNum(val,s,3,1,6)
setNum(val,s,3,2,4)
setNum(val,s,3,7,7)
setNum(val,s,4,6,3)
setNum(val,s,5,3,1)
setNum(val,s,5,4,8)
setNum(val,s,5,6,5)
setNum(val,s,6,1,9)
setNum(val,s,6,7,4)
setNum(val,s,6,9,2)
setNum(val,s,7,6,9)
setNum(val,s,7,7,3)
setNum(val,s,7,8,5)
setNum(val,s,8,1,7)
setNum(val,s,8,5,6)
setNum(val,s,9,5,2)
#n*n個の変数を用意
n = 9
val = [[Int("val[%d,%d]" % (i,j)) for j in range(n)] for i in range(n)]
s = Solver()
#制約を追加
betweenOneToNine(val,s)
distinctRow(val,s)
distinctColumn(val,s)
distinctBlock(val,s)
setProb001(val,s)
#充足可能性を判定、unsatならexit
r = s.check()
if r == sat:
m = s.model()
#印字
for i in range(n):
for j in range(n):
print("%d " % m[ val[i][j] ].as_long(), end="")
print()
else:
print(r)
解説
だいたいこんな戦略でやりました
1. 9*9個の整数型の変数valを用意
2. 全ての変数valにおいて、1≤val≤9
3. 縦列の9個の変数は全て異なる
4. 横列の9個の変数は全て異なる
5. 3*3のブロック内の9個の変数は全て異なる
6. 初期配置されている変数を入力
1. 9*9個の整数型の変数valを用意
- 整数型変数を一つ作るのは以下の通り
x = Int("x")
- 今回の問題を解くには、整数型変数9*9個必要
- これから制約をつっこんでいくソルバーもここで用意
#n*n個の変数を用意
n = 9
val = [[Int("val[%d,%d]" % (i,j)) for j in range(n)] for i in range(n)]
s = Solver()
2. 全ての変数valにおいて、1≤val≤9
- ソルバに制約を追加するのは以下の通り
- この例だと、命題Pと命題Qの積を制約として追加している
s.add(P,Q)
- 今回の問題を解くには9*9個のval全てが1以上9以下であってほしいので以下の通り
#全ての変数valは1<=val<=9であることの制約を追加するメソッド
def betweenOneToNine(val,s):
for i in range(n):
for j in range(n):
s.add(1 <= val[i][j], val[i][j] <= n)
3. 縦列の9個の変数は全て異なる
- 複数の式が異なる値を持つことの制約は以下の通り
- この場合、xとyとzはいずれも異なる値となる
Distinct(x, y, z)
- 今回の問題を解くには9つの縦列の数字はそれぞれ全て異なっていてほしいので以下の通り
#rowがそれぞれ他と値が異なっていることの制約を追加するメソッド
def distinctRow(val,s):
for i in range(n):
tmpList = []
for j in range(n):
tmpList.append(val[i][j])
s.add(Distinct(tmpList))
4. 横列の9個の変数は全て異なる
- 縦列の時とほぼ一緒
- 今回の問題を解くには9つの横列の数字はそれぞれ全て異なっていてほしいので以下の通り
#columnがそれぞれ他と値が異なっていることの制約を追加するメソッド
def distinctColumn(val,s):
for i in range(n):
tmpList = []
for j in range(n):
tmpList.append(val[j][i])
s.add(Distinct(tmpList))
5. 3*3のブロック内の9個の変数は全て異なる
- 縦横列の時からちょっと工夫する
- 今回の問題を解くに9つある3*3ブロック内の数字はそれぞれ全て異なっていてほしいので以下の通り
#ブロックの中身がそれぞれ他と値がことなっていることの制約を追加するメソッド
def distinctBlock(val,s):
for k in range(3):
for l in range(3):
tmpList = []
for i in range(3):
for j in range(3):
tmpList.append(val[3*k+i][3*l+j])
s.add(Distinct(tmpList))
6. 初期配置されている変数を入力
- セッターのようなメソッドを用意しておく
- 第3,4引数で座標を指定
- 第5引数で配置する数値を指定
#あるマス目に任意の数値をセットすることの制約を追加するメソッド
def setNum(val,s,x,y,num):
s.add(val[x-1][y-1]==num)
- 今回の問題に初期配置されている数値をガツガツ入れていく
- しんどい
- もっと賢いやり方をすべき
#数独問題集上級001の問題設定の制約を追加するメソッド
def setProb001(val,s):
setNum(val,s,2,6,1)
setNum(val,s,2,8,8)
setNum(val,s,3,1,6)
setNum(val,s,3,2,4)
setNum(val,s,3,7,7)
setNum(val,s,4,6,3)
setNum(val,s,5,3,1)
setNum(val,s,5,4,8)
setNum(val,s,5,6,5)
setNum(val,s,6,1,9)
setNum(val,s,6,7,4)
setNum(val,s,6,9,2)
setNum(val,s,7,6,9)
setNum(val,s,7,7,3)
setNum(val,s,7,8,5)
setNum(val,s,8,1,7)
setNum(val,s,8,5,6)
setNum(val,s,9,5,2)
結果
- 解が出力されました
1 8 7 6 3 2 5 4 9
5 9 2 4 7 1 6 8 3
6 4 3 9 5 8 7 2 1
4 7 6 2 9 3 8 1 5
3 2 1 8 4 5 9 7 6
9 5 8 7 1 6 4 3 2
2 6 4 1 8 9 3 5 7
7 1 5 3 6 4 2 9 8
8 3 9 5 2 7 1 6 4
まとめ
- Z3を使って簡単な論理問題を解きたかったので
- Pythonで実装しました
- これで数独パズルの懸賞に応募し放題!
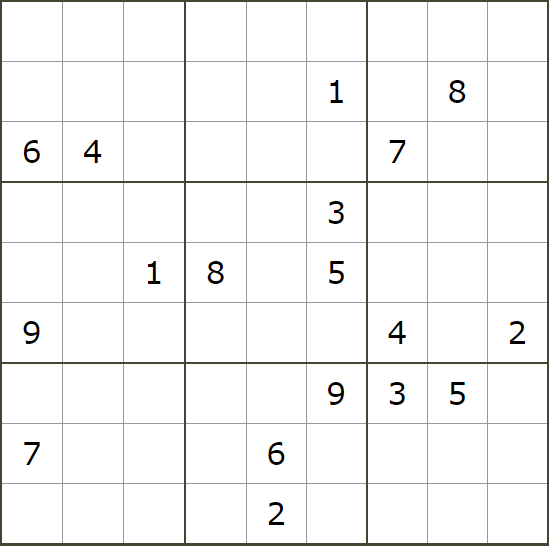
こんな書き方はいかが?
すばらしいです。
ちなみに、時間はどれぐらいかかります。
世界最難問に挑戦してみたら、どうですか?
http://www.tknottet.sakura.ne.jp/sudoku/Difficulty.cgi
私はRで数独を解いたことがあります。
@shiracamus さん
ご提案ありがとうございます!
スマートな実装で大変勉強になります。
Pythonはほとんど書いたことがなく、未熟なコードを公開することを非常に恐れていました。
このような親切な助言をいただけると、非常にありがたいです。
@xuyun19840618 さん
時間は特に気にしていませんでしたが、
pythonなのと、SATではなくSMTであることからあまり速度は期待できないと考えています。
数独の問題に、数値化された難易があることは初耳でした。
機会があれば今回の手法で解いてみたいと思います。
z3のインストール方法がいまいちわからなくて調べてみました.Cannot import z3 in Python #904
Macの場合
$ pip install z3-solverで導入できました.ビルドにはすごく時間がかかりました.
記事のサンプルコードの実行は1秒ちょいでした.
ちなみに
The New Sudoku Players' Forum(SE Top5 No.1)
http://www.tknottet.sakura.ne.jp/sudoku/ASudokuSolver.cgi?IN=000000039000001005003050800008090006070002000100400000009080050020000600400700000
の結果は
7 5 1 8 4 6 2 3 9
8 9 2 3 7 1 4 6 5
6 4 3 2 5 9 8 7 1
2 3 8 1 9 7 5 4 6
9 7 4 5 6 2 3 1 8
1 6 5 4 3 8 9 2 7
3 1 9 6 8 4 7 5 2
5 2 7 9 1 3 6 8 4
4 8 6 7 2 5 1 9 3
でした.
1秒ちょいで解けました.
追記:ー>にてコードをクラス化してみました. https://qiita.com/SatoshiTerasaki/items/bb9f4862ac79cbfa9759