I read a few weeks ago about a study where vitamin D supplementation reduced all-cause mortality rates by 6%. How many years would that add to life expectancy? I wondered.
6% of a 75-year life span would mean 4½ extra years, I thought, naïvely.
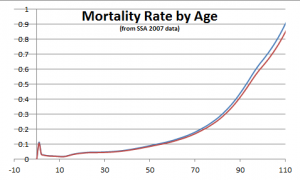
I pulled up a mortality table (from the Social Security Admin) and did the calculation in a spreadsheet. The two lines were barely distinguishable. A 6% drop in mortality only increases life expectancy by 7 months.
What’s going on?
This plot is telling us something deep about the way in which biological aging works. The death rate climbs rapidly with age, and effectively imposes an upper limit on life span that is difficult to circumvent.
If the death rate did not increase with age, then it would be true that subtracting 6% from mortality would add about 6% to life expectancy. That’s where the intuition came from about 4½ years. But with a death rate that increases with age, you “have to work a lot harder” to get an improvement in life expectancy. And in reality, the mortality curve doesn’t just rise with age – it rises at an accelerating rate.
For late life, the mortality curve becomes a wall of death.
The general relationship between mortality and life expectancy
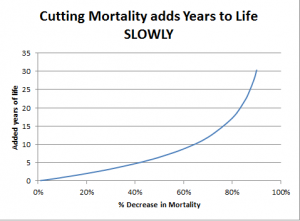
Once I had set up the spreadsheet, it’s easy enough to ask the general question: How much does life expectancy improve for a given change in mortality? The answer I found was: very slowly
To add just 5 years to life expectancy, we would need to slash the mortality rate by more than 40%. This is a counter-intuitive statistic – and a discouraging one. By optimistic accounts, taking a daily aspirin or ibuprofen lowers mortality by 13%. But even this major drop translates to only 2 years. From another perspective, 2 years is a windfall. Aspirin costs practically nothing and imposes minimal risk and less inconvenience.
The optimistic way to see this relationship
There is another perspective on the “wall of death”, about which advocates of life extension have written compellingly. In medical research, we are working piecemeal to chip away at the mortality rate from one disease and another. But if the fundamental rate of aging can be slowed, this will push the curve not down but to the right. This will have as much benefit as many decades of progress in cancer and heart disease.
Caloric restriction offers a bit of this. CR mimetics, therapies that focus on gene expression and signaling may offer a health dividend comparable to the collective product of all of 20th century medical science.
Look at the historical increases in life expectancy. It’s a pretty smooth graph. The conclusion that I draw from this is that its lots of changes that contribute. Either small increases for lots of people (vacination), or large increases for a small number (eg cure for a cancer)
So from that 6% here, 3% there, soon adds up. So far there is no sign of any decrease in the rate, of 1 year extra every 8-9 years.
The evidence that it will stop is called rectangularisation. Life expectancy going up, but maximum life span – 120 years – hasn’t increased.
Thanks, Nick.
Oeppen and Vaupel (http://www.sciencemag.org/content/296/5570/1029.short) have estimated the increase in life expectancy as much faster yet – more than one year of life expectancy increase for each 5 years that pass, citing worldwide “best practices” nations. The “squaring” matured in the 1970s, and since then the progress has been almost entirely at the “back end” of the mortality curve.
In this paper, I estimate about a 15% reduction in mortality rate for doubling serum 25-hydroxyvitamin D concentrations from 55 nmol/l to 110 nmol/l (22 ng/ml to 44 ng/ml). The abstract can be found at http://www.pubmed.gov
Grant WB. An estimate of the global reduction in mortality rates through doubling vitamin D levels. Eur J Clin Nutr. 2011 September;65(9):1016-26.
Thanks, William – I’m very glad to know about this paper, and will study it. Can you tell me in a nutshell why you think you come up with more optimistic estimates than other studies?
Hi,
I use observational studies and do graphical meta-analyses of the findings of odds ratio or hazard ratio vs. 25OHD concentration. I consider case-control studies better than nested case-control studies from cohort studies due to changes in 25OHD concentration with time. See these two open access papers:
Grant WB. Effect of interval between serum draw and follow-up period on relative risk of cancer incidence with respect to 25-hydroxyvitamin D level; implications for meta-analyses and setting vitamin D guidelines. Dermatoendocrinol. 2011;3(3):199-204.
Grant WB. Effect of follow-up time on the relation between prediagnostic serum 25-hydroxyitamin D and all-cause mortality rate. Dermatoendocrinol. 2012;4(2):198-202.
The second paper suggests that increasing serum 25OHD concentration by 20 ng/ml would reduce mortality rates by 28%, which is about twice what I estimated, but supports my estimate.
In addition, I look very carefully at randomized controlled trials, since those with vitamin D are generally not conducted properly. See:
Open Access Article
Why randomized controlled trials of calcium and vitamin D sometimes fail
Joan M. Lappe and Robert P. Heaney
Pages 95 – 100
http://dx.doi.org/10.4161/derm.19833
Abstract | Full Text | PDF
http://www.landesbioscience.com/journals/dermatoendocrinology/toc/volume/4/issue/2/
On the other hand:
http://www.cmaj.ca/content/early/2012/11/05/cmaj.120233
See the comments posted regarding this paper, including one from me.
The study design makes it hard to separate genetic from environmental factors. Genetic differences in the way vit D is used may account for the differences in blood levels. Still, it is always worthwhile to fully consider the opposition case. The alternative hypothesis to consider is that low vit D levels are a result of disease, not a cause. I think that Dr Grant effectively refutes this view.
How do you do those calculations? If the study notes a decrease in mortality would the calculation only be spread over the onset of the study and the age of death?
I made the (unrealistic, simplifying) assumption that the same percentage decrease in mortality continues at all ages. Then the calculation can be done simply in a spreadsheet.
The “easy” improvements include approving the cancer cures forbidden for lack of a patented drug to ensure monopoly profits, eliminating the merely profit oriented GMOs, rejecting aspartame and other sources of methanol, to which humans are uniquely sensitive. When these inexpensive things are done, we will have lowered our health care costs, so we can afford to pursue rejuvenation mechanisms with more vigor. On the methanol issue, see WhileScienceSleeps.com and the similarly titled book by Prof. Woodrow Monte.
Pingback: Death Rates Rise for Young White Americans Too | Daily Blue Planet