直感とは、理性を働かせることなく感覚的にただちに物事をとらえることです。
「直感を信じる」ことは、一見すると不合理な行動に感じられるかもしれませんが、直感を支えているのはそれまで生きてきた何億秒という時間の中で培われてきた経験に他なりません。
そう考えると、長い月日の中で得られた体感的統計こそが直感の正体であり、直感を信じることは意外と合理的な判断であることが多いのです。
ただしここで注意しておきたいのが、世の中には
「直感的に感じる確率」と「実際の確率」が大きく異なるケースも多数存在するということ。
このようなケースで直感だけを信じてしまうと、思わぬ損失につながってしまいます。
逆に言えば、こういったケースの存在を知っておくだけで、簡単に直感の精度を高めることができるんです。
今回は、そんな例をいくつか見ていきましょう。
photo credit: Lali Masriera
目次
直感的確率と実際の確率が異なる4つのケース
ケース(1)くじ・ガチャ・確率機の当たる確率
Gashapon / Dick Thomas Johnson
まずは初級編。
1/100の確率で当たるくじがあったとします。
ある日、A君はこう言いました。
「俺、今までこのくじを通算100回も引いたのに、1度も当たったことが無いんだ。俺って、ものすごく運が悪いんだな…」
Q:彼は本当にものすごく運が悪いのでしょうか?
皆さんは、どう感じましたか?
直感で考えると「1/100の確率で当たるなら100回も引けば大体当たるだろうし、A君はものすごく運が悪いな」と思ってしまうかもしれません。
しかし実際に計算してみると、
1/100の確率で当たるくじを100回引いて1度も当たらない確率は、なんと約36.6%もあるんです。
「サイコロを1回振って2以下が出る確率(≒33.3%)よりも高い」と考えると、意外とよくあることなのだと分かります。
当たる確率の低いくじやガチャに何度も挑戦する時は、覚悟が必要ということですね。
ケース(2)クラスに同じ誕生日のペアがいる確率
次は、誕生日の偶然について。
生まれが「うるう年」ではない、ある学年の話。
そのクラスには23人の生徒がいます。ある日、クラス全員の誕生日を聞いたところ、BさんとC君の誕生日が同じだと分かりました。
「BさんとC君って同じ誕生日なの!?同じクラスで1/365の確率を引き当てるなんて、すごい運命だ!」と皆おおはしゃぎ。
しかし、先生にこの話をすると「よくあることだよ」と冷めた態度でした。
Q:先生の言う通り、これは本当によくあることなのでしょうか?
たしかに「BさんとC君が同じ誕生日」である確率は1/365であり、珍しいことのように思えます。
しかし今回の話は「同じクラスの23人全員の誕生日を聞いたら、同じ誕生日のペアがいた」というのがポイント。
実は、23人のクラスに同じ誕生日のペアが1組以上いる確率を計算してみると、約50.7%もあるんです。
直感ではかなり低い確率に思えても、実際には「100クラスあれば50クラスで起きる」ことだったのです。
参考:誕生日のパラドックス
実際に皆さんと同じクラスや部署にいる全員の誕生日を聞いたら、1組は同じ誕生日のペアがいるかもしれませんよ。
ケース(3)病気の検査が正しい確率
Cast Aluminum Doctor with Stethoscope (New Kensington, PA) / takomabibelot
ちょっと難しくなります。
あるところに、99%正しい検査ができる医師がいました。
その医師に、「あなたが20万人に1人の病気にかかっているか」を検査してもらったところ、その病気にかかっているという検査結果が出ました。
Q:このとき、あなたが本当にその病気にかかっている確率は何%でしょうか。
多くの方が「99%正しい検査ができる医師なんでしょ?なら、99%病気なんじゃないの?」と思ったのではないでしょうか?
でも、違うんです。
実は、「20万人に1人の病気にかかっている」という検査結果が出ても、本当にその病気である確率はわずか0.049%しかないのです。
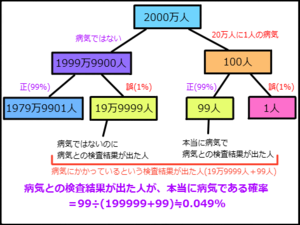
下の図を見てください。
まず検査対象が全体で2000万人いたとします。
この内、実際に20万人に1人の病気にかかっている人は100人。その中の99人に「病気にかかっている」という正しい検査結果が出ます。
一方、残りの1999万9900人はこの病気にかかっていませんが、その中の1%=19万9999人に「病気にかかっている」という誤った検査結果が出てしまいます。
つまり、合計200098人に対して「20万人に1人の病気にかかっている」という検査結果が出るものの、本当にその病気にかかっている人はその中の99人だけということになります。
そのため、「20万人に1人の病気にかかっている」という検査結果が出ても、本当にその病気である確率はわずか0.049%しかないのです。
参考:ベイズ推定
この事例からは、どれだけ精度の高い検査であっても「20万人に1人の病気である」との検査結果が誤って出てしまうケースは意外と多いということが分かります。
多くの医師が「精度の高い検査であっても気を抜かずに何度も再検査する」のも納得ですね。
「目の前の数字に騙されず、冷静に確率を分析する大切さ」を痛感させられます。
ケース(4)運用先の選定
Piggy Bank / free pictures of money
今、あなたは次の2つの運用先のどちらかの方法で100万円を運用しようと考えています。
運用期間は20年。①の確率変数は正規分布に従うものとします。
①:平均年利2%(複利)・標準偏差5%の運用機関
②:20年後に90%の確率で140万円、10%の確率で95万円になる運用機関
Q:より安全に資産をふやしたい場合、①と②のどちらで運用するべきでしょうか?
※標準偏差は、バラツキを表す数字です。①は「基本的には毎年-3%~+7%をウロウロして、たまに-8%~+12%になることもある」くらいに考えて下さい。
①は毎年目減りする可能性があり、運悪く「-1%」を20年引き続けたら18万円近く損するかもしれません。
一方で②は高確率で40万円も得をし、運が悪くても5万円の損で済みます。
そう考えると、「①はリスク志向、②は安全志向な運用先」に見える方もいると思います。
しかし、実際はそうとも言えません。
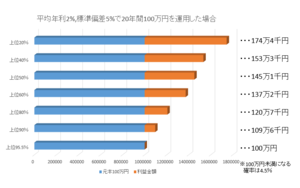
上のグラフは、平均年利2%(複利),標準偏差5%で100万円を20年運用した場合の運用結果を算出したものです。
実際に計算してみると、20年後に140万円以上になる確率が50%以上あり、逆に100万円未満になる確率は4.5%しかないことが分かります。
「②では95万円になる確率が10%もある」一方で「①では100万円未満になる確率は4.5%しかない」と考えると、むしろ「①の方が安全志向、②の方がリスク志向な運用先」と考えられます。
もちろん、「0.1%でも90万円以下になる可能性があるのは嫌だ!」という方にとっては②の方が安全です。
ただ、100万円未満になる(=元本割れする)確率を最小限にしつつ資産をふやす、という意味では①の方が安全と言えるのです。
現実の運用では計算通りにいくとは限りませんが、この例で優劣を判断したい場合における確率計算の重要性は伝わったかと思います。
元本割れする可能性を最小限にしつつ資産を増やしたいなら、10%の確率で95万円になる②よりも、100万円未満になる確率が4.5%である①の方が安全。
確率論を身につけて、直感力を高めよう
いかがだったでしょうか。
確率論と言うと「頭の良い人だけが勉強すればいいんじゃない?自分には関係ないよ」と思ってしまう方もいるかもしれませんが、実際にはこのように確率論が役に立つケースは身近にたくさん存在します。
初めに述べたように、直感を信じて行動することは意外と合理的な判断であることが多い一方で、今回取り上げた話のように実際に確率を計算してみると直感と異なるケースも少なくありません。
確率論を利用して「直感的な確率と実際の確率のズレ」を減らした上で、直感を信じる。
それが「運の良い人」になるための第一歩だと、ぼくは思います。
こちらもオススメ!
【運ゲーとは?】確率は収束するが、運は収束しない【前編:なぜ確率は収束するか】 | アタリマエ!