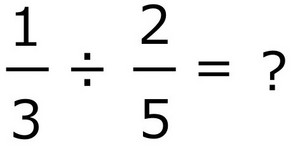分数の割り算をするときは、
割る数をひっくり返してかける(=逆数をかける)ことで答えが求まります。
しかし、「分数で割るとはどういうことなのか?」が直感的に理解しにくいせいで、
ここでつまづいてしまう小学生も少なくありません。
実際、小学生に「分数の割り算をするときにひっくり返すのはなんで?」と質問されて、
答えに窮する親御さんも多いのではないでしょうか。
どうも、tooda(@atarimae55)です。
今回は、「分数の割り算では逆数をかける」理由を説明する3つの教え方を紹介していきます。
この3つのうち、1つでも納得のいくものがあればそれで十分なので、「自分にあった考え方はどれかな?」と考えながら読んでみてください。
目次
①分数の割り算を「分数の分数」に変形する教え方
2÷5=2/5といったように、割り算は分数に変形できるという特徴があります。
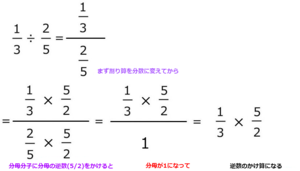
これを分数同士の割り算に応用すると、下のような「分数の分数」に変形することができます。
割り算を分数に変形したら、次はこの「分数の分数」をシンプルな形に直すことを考えましょう。
分数をシンプルにするには、「分母と分子にそれぞれ『分母の逆数』をかけること」で分母を1にするのがコツです。通分や約分と似た作業ですね。
※逆数:ひっくり返した数のこと。3/7の逆数は7/3
今回は分母が「2/5」なので、
「2/5」の逆数である「5/2」を分母と分子それぞれにかけていきます。
こう考えてみると、分数同士の割り算がなぜ逆数のかけ算になるのかが分かりやすくなります。
②シンプルな分数の割り算で、「分ける」で考える教え方
分数の割り算が分かりにくい原因は、
「2で割る」や「7で割る」と違って「2/3で割る」ことが想像しにくい点にあります。
そこで、8/3÷2/3といったシンプルな答えになる分数の割り算から「分ける」イメージで考えてみましょう。
たとえば、6÷2=?は
「6ℓの水を一人あたり2ℓずつ分けると、何人に分けられる?」を表す数式でもあります。

今度はこれを、8/3÷2/3に当てはめます。
「8/3ℓの水を一人あたり2/3ℓずつ分けると、何人に分けられる?」
これを表す数式が、8/3÷2/3=4となります。
このように「一人あたり2/3ℓずつに分ける」ことで、「水のℓ数の3/2倍の人数」に分けられるようになるんです。
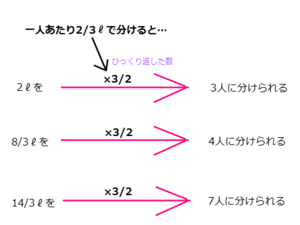
こう考えると「分数で割ること」がイメージしやすい上、分数の割り算が逆数のかけ算になることも分かりやすくなります。
③「コップ1杯あたり」で考える教え方
②の教え方は、答えが整数になるときしか使えません。
答えが分数になる式でも使えるのが、「コップ1杯あたり」という考え方。
たとえば、6÷2は次のように考える事ができます。
「6個のりんごで、コップ2杯分のりんごジューズがつくれる。
このとき、りんごジュースコップ1杯あたり何個のりんごが必要か?」
答えは6÷2=3個ですね。
このように、
割り算は「コップ1杯当たり何個の果物が必要なのか?」を表す数式と考える事ができます。
今度はこれを、1/3÷2/5に当てはめて考えてみましょう。
「1/3個のグレープフルーツで、コップ2/5杯分のグレープフルーツジューズがつくれる。 このとき、グレープフルーツジュースコップ1杯あたり何個のグレープフルーツが必要か?」
これが、1/3÷2/5です。
2/5杯分のジュースを作るのに1/3個のグレープフルーツを使うのですから、
1杯分のジュースを作るには、1/3個の「5/2」倍のグレープフルーツが必要なはず。
これは、逆数のかけ算をしているのと同じことです。
だから、「1/3÷2/5=1/3×5/2」となるんです。
分数の割り算はひっくり返してかける理由:まとめ
①2÷5=2/5といったように、割り算は分数に変形できる
→分数の割り算を「分数の分数」に変形してから、分母が1になるように変形すると、逆数のかけ算になる
②分数で割るをイメージしたい時は、「一人あたり○ℓずつに分ける」でイメージする
→8/3÷2/3は「8/3リットルの水を1人あたり2/3ℓずつに分けると、何人に分けられるか?」で考えると逆数をかける理由がイメージしやすい
③割り算は「コップ1杯当たり何個の果物が必要なのか?」を表す数式と考える事ができる
→コップ1杯当たり何個の果物が必要かを実際に考えると、実質的に逆数のかけ算をしているのと同じ
以上3つに、求めていた答え方はありましたでしょうか?
この記事が、分数の割り算を理解する助けになれば幸いです。
こちらもオススメ!
円周の求め方。円周率とはなにか。なぜ無限に続くのかを説明。小学生にも分かる割り切れない理由
ゼロで割ってはいけない理由を、割り算の定義から説明するとこうなる